電気で計算する方法
目次
回路の名前
ここまで、並列スイッチ回路とか、直列スイッチ回路とか、スイッチの並び方で回路を呼んできた。
長い名前なので、もっと短い名前を用意しよう。
…というか、今から書くのが一般的な名前だ。
いきなり専門用語を使うと難しそうに見えるのでここまで書かなかっただけだ。
直列スイッチ回路は、AND (アンド)と呼ばれる。英語で「共に」という意味だ。
回路では、スイッチを両方「共に」ON にしないと、電球が点かなかった。
並列スイッチ回路は、OR (オア)と呼ばれる。英語で「どちらか」という意味だ。
どちらかのスイッチを ON にすれば、電球が点いた。
3路スイッチ回路は、XOR (エックスオア)と呼ばれる。
英語で…ちょっと難しいけど、これは exclusive OR の略で、「どちらか片方だけ」というような意味合いだ。
どちらか片方だけ 1 なら 1 、両方 0 か 1 なら 0 になる。
ちなみに、EOR とか EX-OR と略される場合もある。
 もう一つ、今回の話には出てないけど、NOT (ノット)というのもある。「違う」という意味だな。
もう一つ、今回の話には出てないけど、NOT (ノット)というのもある。「違う」という意味だな。
他の計算と違って、計算に使う数は1つだけ。
0 を計算すると 1 になり、1 を計算すると 0 になる。「違う」数になるんだ。
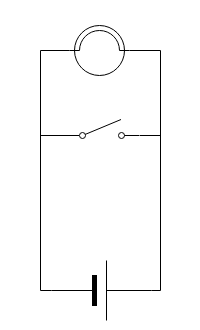
回路は右図のような感じだけど、3年生の知識では、何が起きるか予想できないだろう。
電球って、光るのにすごいエネルギーが必要で、電気にとっては「通るのが面倒」なんだ。
そこしか道がないなら仕方なく通るけど、もっと楽な道があれば、多くはそちらに流れてしまう。
右図でスイッチを ON にすると、電球を通らない道が出来上がるので、電球には電気が流れなくなってしまう。
だから、スイッチ ON で電球が消える。NOT の計算になる。
AND OR XOR NOT 。コンピューターの基本回路は、実はこの4つしかない。
小学校3年生の知識でどれも(NOT は少し例外だけど)理解できるものだ。
こうした基礎回路を、まとめて「論理回路」と呼ぶ。
あとは、これを複雑に…気が遠くなるほど複雑に組み合わせれば、コンピューターができる。
複数桁への拡張
複雑に組み合わせればコンピューターができる、と言われても、どう組み合わせればいいのか想像もつかないだろう。
もう少し簡単なところで、2進数複数桁の足し算回路を作る方法を示そう。
ただ、ここでは回路図は示さない。本当に複雑になるからだ。
言葉で概要を示すだけだけど、「なんとなくわかった」気になってくれればそれで充分。
まず、先に書いたように、繰り上がり付き2進数1桁を作るだけでも、XOR と AND を組み合わせる必要があった。
二つの回路それぞれにスイッチがあるのだけど、これは連動して動くものだとしよう。
物理的に、スイッチを板か何かで一緒に動くようにしてしまえばいい。
XOR と AND が同時に動けば、1桁の足し算としては XOR が、繰り上がり部分の計算としては AND がそのまま使える。
これで 1bit の足し算ができた。
次に、これを複数桁にしたい。しかし、ただこの 1bit 足し算をたくさん並べればいい、ということではない。
ただ並べただけでは、「繰り上がり」が正しく計算されないから。
複数桁の計算では、繰り上がりを正しく上の桁に足してやらないといけない。
しかし、ここで問題が出る。
今まで、繰り上がりの回路は、結果を電球で示すことにしていた。
でも、上の桁に足そうと思ったら、スイッチでなくてはならない。電球はスイッチにならないから、「組み合わせる」ことができない。
そこで、小5で習う「電磁石」に登場してもらおう。
電球の代わりに電磁石を入れる。電磁石は、電気が流れていないとただの鉄の棒、電気が流れると磁石になる。
この磁石で、鉄板を引き付けよう。
先に、電磁石は普段は「ただの鉄の棒」と書いたが、鉄の棒なので電気を通す。
そして、鉄板を引き付けてくっついたら、鉄板を通じて電気が流れていくようにしよう。
これは、スイッチとして使える。電気によって ON / OFF できるスイッチ。
リレースイッチ、という名前がついている。
実際、初期の電気計算機には、リレーを使って作られているものがあった。
リレーを使えば、多くの論理回路を組み合わせられる。
さて、2進数複数桁の足し算回路の作り方を示そう。
まず、先に書いた通り、XOR と AND を組み合わせて、繰り上がり付きの 1bit 足し算を作る。
この回路は、2進数1桁を2つ入れると、1桁の「答え」と、1桁の「繰り上がり」を出す。
この回路を「半加算器」と呼ぶ。
加算というのは足し算のことだけど、「半加算器」は足し算を半分だけやっている。
半分、というのは、下からの繰り上がりを計算してないから。
・足し合わせる2つの数の、特定桁の2進数1桁を半加算器で計算する。
・半加算器の答えと、下の桁からの「繰り上がり」を、半加算器で計算する。
この「答え」は、結果1桁として使われる。
・上に書いた2つの半加算器の「繰り上がり」を、OR に入れて計算する。
この結果を、上の桁への「繰り上がり」とする。
これだけだ。
最後に繰り上がりを2つ「足して」いるのだけど、ここには半加算器を使う必要はない。
OR で良い理由を示そう。
2進数1桁を2つと、下の桁からの繰り上がり1桁、つまりは2進数1桁3つを足すと、最大でいくつになるだろうか?
1 + 1 + 1 = 11
ここで、11 は2進数だ。2桁になっている。
3つの数を足しても、1つ上の桁への繰り上がりしか起こらない、という意味でもある。
ということは、繰り上がりの計算で、さらに繰り上がりが生じることはない。
繰り上がりを考慮した「半加算器」を使う必要はなく、単純な OR でいい。
半加算器2個と、OR が1個。これで2進数の「完全な」計算が行える。
これを全加算器と呼ぶ。
あとは、全加算器を必要な桁数分並べれば、2進数複数桁の足し算回路が出来上がる。