平方根(ルート)の求め方
当ページを読んで、「高校生当時、レポートを書くのにタイガー計算機を使っていました」という助川さんから、開平(平方を開く、つまり平方根=ルートを求める)計算の方法を教えてもらいました。
ネット上を調べたところでは、あまりこの方法の情報がなかったので、紹介しておきます。
追記 2011.12.08
「もっと簡単な解説を」という意見が多いので…余りに多いので…別ページに書きました。
「簡単に」と「簡潔に」は同居しない。基礎から書いているので、非常に長い説明です。
このページの説明だけでは理解できない、という方はどうぞ。
まず、わかりやすい例として 25 の平方根(√25)を求める方法から。
計算手順の基本は、「奇数を順次引いていく」だけです。これだけで平方根が求まります。
| 25 | -1 | =24 |
| 24 | -3 | =21 |
| 21 | -5 | =16 |
| 16 | -7 | =9 |
| 9 | -9 | =0 |
この場合、5回で計算が終了するので、√25 = 5 です。
このことの数学的な意味を、図形で検証します。
 最初に「1を引く」ということは、図形の左上の■の部分を引く、ということです。
最初に「1を引く」ということは、図形の左上の■の部分を引く、ということです。
つづいて、「3を引く」ということは、左上の■を囲む、□の3つ分を引く、ということです。
同様に、5を引くのはさらに周囲の■部分を引くこと、7は□部分を…と続けていって、9を引いたら結果が「0」になりました。
つまり、図形的には上の5×5の、25マスを埋めきったことになります。√25 = 5 です。
つづいて、もっと大きな数でも平方根を求めてみましょう。この場合、10×10=100 であることを利用して、2桁づつ数値を区切って計算を行います。
例題として、√529を求めてみます。まず、下から2桁づつ区切って、5 と 29に分かれていると考えます。
| 5 | -1 | =4 |
| 4 | -3 | =1 |
ここでこれ以上引けなくなりました。2回で終了なので、答えの上の桁は2です。つづいて、下の桁である「29」をくっつけて、129が残っていると考えます。
このとき、「引く数」としては、3 に 1 を足した 4 を上の桁にもってきて、41 からはじめます。(このことの意味は後で解説します)
| 129 | -41 | =88 |
| 88 | -43 | =45 |
| 45 | -45 | = 0 |
ここで終わりです。上の桁が2、下の桁が3なので、√529 = 23 です。
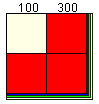 こちらも図形で検証してみましょう。
こちらも図形で検証してみましょう。
最初に上の桁で1を引くということは、10*10=100 を全体から引いていることになります。図形の左上の部分です。3を引くのも、図形で赤く塗った 300を引くのと同じこと。
ここで、それ以上引けなくなりましたので、引く図形の面積を「細かく」します。
下の桁にすぐにうつる前に、いま計算が終わった「上の桁」の図形について見直しておきましょう。
赤い四角形は、縦横2個、左上が無い形で「3個」ありました。これが例えば、赤の外側にさらに5個の四角形を並べる場合だと、縦横は3個になります。n 個の四角形を並べる時は、常に縦横には (n+1)/2 個並んでいることになります。
では、下の桁の計算にうつるために、並べる四角形のサイズを縦横 1/10 にします。並べる数は 10 倍になります。
赤い四角形は、縦横2個並んでいましたので、1/10 サイズで考えると、同じ場所に縦横20個の四角形を並べることができます。そのまま少しずらして、赤い四角形の「外側」、図形では青い細い線で示される部分に持っていくと、角の部分にもう一つ必要になるので、縦に 20 個、横に 20 個、角に 1 個、合計では 41 個必要です。
この計算は、もっと簡単にできます。基本的に、上の桁の計算が n で終わったとき、次の桁では (n+1)*10+1 から計算が始まります。タイガー計算機的には「つまみを 1 上げて、桁をずらして、新しい桁のつまみを 1 にセット」です。計算ですらない機械的操作です。これで、下の桁の計算準備が整いました。
青の 41 個を引いた後は、基本に従って順次奇数を引いていきます。緑の部分は 43、黄色は 45 を引くことになります。
つまり、最初に100単位の大きな領域を引いておいて、引けなくなったら細い領域を徐々に広げていく…という戦略で、図形全体を求めているわけです。
例では3桁でしたが、同じ作業の繰り返しで、もっと大きな桁数でも求められます。
上の2つの例では、あえて整数で割り切れる数を例題としました。しかし、割り切れない数でも求めることができます。
話としては単純で、固定小数点演算を行うだけですが…固定小数点ということは、結局のところ整数演算ですから。この場合、桁を下にずらしていくときには、見えない 00 が入っていた、と考えて続けます。
√13を求めてみましょう。あらかじめ答えを書いておくと、3.60555128 になるはずです。
| 13 | -1 | =12 |
| 12 | -3 | = 9 |
| 9 | -5 | = 4 |
最初の桁は3です。これ以上は続けられないので、桁をずらします。ここから先は小数点以下の計算になりますが、求める数の小数点以下は「00」が続いていると考えます。
| 400 | -61 | =339 |
| 339 | -63 | =276 |
| 276 | -65 | =211 |
| 211 | -67 | =144 |
| 144 | -69 | = 75 |
| 75 | -71 | = 4 |
2桁目は6です。これ以上は続けられないので、さらに桁をずらします。
しかし、ここで 400 - 721 を行おうとすると、1度も計算できません。3桁目は 0 です。
次の桁は、少し通常と異なる手順となります。普通なら、「最後に引いた」数に 1 を足してから桁を上げますが、最後に引いた数がありません。
この場合、最後に引く「予定だった」数から 1 を引いてから、桁を上げます。
このことの意味を考えて見ましょう。そもそも、引く数を奇数にしているのは、図形的に考えた場合に「角」の部分があるためです。
十分に埋まった場合は、図形的には既に説明したとおりに、四角形の大きさを小さくして(つまり、全体の桁を上げて)作業を進めます。このとき、引く数は図形で考えれば、それまで埋めた正方形の「2辺」の外側に移動します。
しかし、「引けなかった場合」は、すでに移動は考慮済みなので、そのまま四角形の大きさをさらに小さくするだけです。
単に 10 倍してしまうと、角の 1 個も 10 倍することになってしまうため、正しくありません。なので、先に 1 を引いてから 10 倍し、その後で改めて 1 を足します。(タイガー計算機的にはつまみの操作と桁ずらしの機械的作業である、というのは先に書いたのと同じです)
では、実際の計算をして見ましょう。先に書いたように、前の計算は 721 を引く予定で引けませんでしたから、次の引く数は (721-1)*10 + 1 で 7201 になります。
| 40000 | -7201 | =32799 |
| 32799 | -7203 | =25596 |
| 25596 | -7205 | =18391 |
| 18391 | -7207 | =11184 |
| 11184 | -7209 | = 3975 |
4桁目は5です。同様に、さらに桁をずらします。
| 397500 | -72101 | =325399 |
| 325399 | -72103 | =253296 |
| 253296 | -72105 | =181191 |
| 181191 | -72107 | =109084 |
| 109084 | -72109 | = 36975 |
ここまでで、√13 = 3.6055 までは求められました。さらに続ければ、もっと下の桁まで求められます。
手計算の手順を見ていると、引き算の桁がだんだん大きくなったりして面倒くさそうに見えるかもしれません。
しかし、タイガー計算機では、引き算はクランクを回すだけで完了します。回した回数は自動的にカウントされるので、結果もすぐに読めます。
桁をずらす作業も、最初からその機構が作りこまれていますし、奇数を順次入れる、という作業も、引く数を設定するレバーに指を掛けたまま、クランクを回すごとに2目盛り下にずらす、ということを続けるだけです。
そう考えると、ここで紹介したアルゴリズムが、非常にタイガー計算機向きに使いやすい方法であることがお分かりいただけると思います。
平方根を求めるアルゴリズムはほかにも数多くありますが、計算に使う「道具」にあわせて使いやすい手法を考え出した知恵には、本当に頭が下がる思いです…
当初、助川さんから頂いたメールは、検算して「確かに計算できそうだ」とはわかっても、なぜそれが平方根の計算になるのか理解できませんでした。助川さんも「実際そのように計算していた」というだけで、意味までは理解しておられませんでしたし…
そのままでは記事にはできないと思い悩んでいたところ、妻がいっしょになって考えてくれ、数学的な意味を見出してくれました。しかし、計算手順を知らなければその作業もできなかったでしょう。
貴重な情報をありがとうございました。助川さんと自分の妻に (^^; 感謝しつつ記事を締めくくります。
追記 2009.09.03
ここに書かれた方法は、タイガー計算機で使用するにはわかりやすい方法ですし、手計算で計算するにも直感的に理解しやすい方法ではあります。
しかし、直感的で判りやすいためか、「コンピューターでの平方根の計算方法」としてのリンクで参照されることが増えてきました。プログラムで生計を立てている身からすると、それはちょっと違うような…
コンピューターで計算するのであれば、手順は多少面倒でも、計算回数が少ない方法が適しています。古典的なところではニュートン法などを調べてみるとよいかと思います。
追記 2010.11.03
ここに書かれたアルゴリズムで、√2を30桁まで計算してみてほしい、と言う要望を頂いたので、別ページに書きました。
その計算の最中に、「引けない場合」の処理について言及が必要だと考えたため、このページの計算サンプルを改めました。ページ作成当初から√2を例題としていましたが、「引けない場合」が初期に現れる√13を例題とするようにしました。