目次
2013-10-14 ブノワ・マンデルブロの命日(2010)
2014-04-04 ジョン・ネイピアの命日
2014-06-19 ブレーズ・パスカルの誕生日
2015-04-04 ジョン・ネイピア 命日(1617)
2015-08-31 夏の終わりの素数
2015-09-07 ruby で数値演算
2015-10-31 ロナルド・グラハム 誕生日(1935)
2016-02-03 ガストン・ジュリア 誕生日(1893)
2021-01-29 微分積分いい気分
2021-03-16 暮らしの中の微分積分
2021-04-01 異世界転移の方法
2021-06-21 ３次元回転
今日はブノワ・マンデルブロの命日。
2010年に亡くなりましたね。もう高齢だったからいつか死ぬのは当然でしょうが、死んだときはちょっとショックでした。
氏の偉業をちゃんと解説したい…と数学（算数？）ページなんて作りましたが、忙しくて頓挫したまま。
マンデルブロ氏の偉業は、数学に「フラクタル」と呼ばれる一分野を開拓したことです。
しかし、この話、案外深いのです。
話は1900年ごろにまでさかのぼります。
1800年代（19世紀）は数学が急速に発達した時代でした。
しかし、世紀が変わってこのままでよいのか、という問題提起が、多くの数学者からなされています。
そのうち一つに、次のような疑問がありました。
数学は、もともと古代エジプトで自然と共に暮らすために生まれた知恵でした。
毎年氾濫するナイル川は、氾濫により豊かな土壌をもたらしてもくれます。
そのため、古代エジプトの人々は、氾濫することがわかっている地域で農業を営んでいました。
問題は、毎年の氾濫後に、どこの土地が誰のものかがわからなくなってしまうこと。
この混乱を避けるために、最初の幾何学が生まれました。
土地を区画整理し、毎年同じように農業が営めるようにしたのです。
その後数学は発達しました。
しかし、その発達とともに、自然からは乖離したように見えます。
人類は、微分積分を手に入れました。しかし、それで美しい雲を、森の木々を、蝶の模様を、表現することはできたのでしょうか？
数学において、「連続性」は非常に重要な意味を持ちます。
連続性とは、すべての点で微分可能、と言い表すこともできます。
…難しいですね。もっと簡単にいえば「どこを見ても滑らか」ということです。
ところが、自然物はそうではありません。葉っぱは大抵先端がとがっていますし、枝もいたるところが尖っています。雲は全体にとらえどころがありません。
極論すれば、どこひとつ滑らかな場所なんてないように見えます。
このような対象を、微分積分を究極の武器とする（当時の）数学で表現することはできない、というのが、1900年ごろの数学批判の根底にありました。
僕は数学史には詳しくないので間違いもあるかもしれませんが、おそらく上記の「問題提起」をうけて、多くの学者が自然の記述方法を考案しています。
鍵は「非連続性」にありました。
…数学者っていうのは極端で、「どこでも滑らか」ではダメだ、となると、「どこをとっても滑らかな場所が見つからない」ようにしようとします。
（どちらも「すべての場所が均質で特別な場所がない」と言う点では同じで、極端に走ったわけではないのですが）
1900年の初頭ごろ、世界中で多くの数学者が「どこをとっても非連続」な図形を考案しています。
ダフィット・ヒルベルト(1862～1943)が1891年に発表した、ヒルベルト曲線。
高木貞治(1875～1960)が1903年に発表した、高木曲線。
ヘルゲ・フォン・コッホ(1870～1924)が1904年に発表した、コッホ曲線。
ヴァツワフ・シェルピンスキー(1882～1969)が1915年に発表した、シェルピンスキーのギャスケット。
NASA物理学者らのグループが1967年に発表した、ドラゴン曲線。
などなど、他にもたくさんあります。
これらは、ただ非連続なだけでなく、「どこを取り出しても、全体と同じような形をしている」という特徴を持っています。
このことを「自己相似性」と言います。
この新しい概念は、自然を表現するための一歩目でした。
たとえば、コッホ曲線を組み合わせると、コッホ切片と呼ばれる雪の結晶のような形が出来上がります。
コッホ曲線は、ただの「直線」に、一定の操作を繰り返すことで得られる図形です。
同様の操作を行うことで、木を表現したり、シダの葉を表現したりできることが知られています。
同時代の数学者に、ガストン・ジュリアがいます。
恐らく、彼も同じような作図を試みたのではないかと思うのですが、彼の手法は少し変わっていました。
先にあげた図形は、すべて「図形に対し、繰り返し操作を加える」ことで描かれます。
しかし、ジュリアは「座標をパラメーターとした数式を繰り返し計算する」と言う方法で図形を描いたのです。
もう少し詳しく説明しましょう。
グラフには、縦軸と横軸があります。グラフ上のある一点は、縦座標と横座標、という「二つの数値」で表現できます。
このとき、この二つの座標を、一定の方法で計算します。計算し続けます。
すると不思議なことに、計算のたびに「数が大きくなっていく」点と「あまり変わらない」点の二つに分かれるのです。
二つに分かれるのは、「ある計算」が自乗を含むためです。
1よりも小さな点を自乗すると、どんどん 0 に近づきます。
1よりも大きな点を自乗すると、どんどん 0 から遠ざかります。
点の座標でいえば、単純に近づく、遠ざかる、と言うのではなく、位置を変えていくことになります。
図形を計算することで別の図形を作り出すことを「写像」と言いますが、ジュリアの計算では、計算のたびに写像を作り出すことになります。
そして、この写像は「中心(0)からどんどん離れる」場合と「中心の周囲を動き回る」場合があるのです。
ジュリアは、遠くなる点は捨て、いつまでも周囲を動く点をプロットしました。
１つの点について「遠くならない」確認のために 100回程度の計算を行い、それを縦横 100地点くらいづつ…100*100*100 で百万回くらい計算を行うと、やっと一つの図形が完成します。
完成した図形（ジュリア集合と呼ばれます）は興味深いものでした。
「計算のたびに中心の周囲を動き回る」ということは、中心付近の点にはなんらかの類似規則があることになります。
図形にはこの規則がはっきりと表れ、全体と一部が似た形になる、「自己相似性」を持っていたのです。
しかし、ジュリアの手法は時間がかかりました。
面白い研究ではありましたが、何かの役に立つわけでもなく、世の中から忘れ去られます。
1950年代、ブノワ・マンデルブロは、経済学を研究していました。
ここで、株価の動きには「全体を縮小したような動きが細かな部分に見られる」という自己相似性に気づきます。
彼は 1900年代初頭に行われた研究を再発見し、これらをまとめ上げる研究を行います。
どこをとっても不連続であり、全体と一部が似ている…こうした図形に「フラクタル」と名前を付けます。
（フラクタルとは、「細かな破片」の意味をもつラテン語に由来する造語）
1970年ごろ、彼はジュリアの手法にも興味を持ちました。
ジュリアの時代には手回し計算機しかありませんでしたが、マンデルブロの時代にはコンピューターがあります。
コンピューターの圧倒的なパワーでジュリア集合を計算してみようとします。
経緯は省きますが、マンデルブロは最初に「ジュリア集合世界の俯瞰図」を作ろうとしました。
当時のコンピューターでは、１００万回の計算はまだ時間がかかるもので、手始めに面白そうな場所を探し出そうとしたのです。
しかし、この「俯瞰図」こそが新しい発見でした。ジュリア集合の数式を少し変化させ、特徴の出やすい点だけを試算したカタログを作ろうとしたのですが、このカタログはジュリア集合以上に興味深い図形となったのです。
ジュリア集合は、６つの計算パラメーターを持ちます。どのパラメーターを変えても違う画像を生じるため、全体の把握は簡単ではありません。
しかし、マンデルブロの作った図形（マンデルブロ集合）は、パラメーターが２つしかないにも関わらず、ジュリア集合と同じような挙動をしめし、細かな部分を見るとジュリア集合にそっくりの図形が現れていたのです。
ジュリアは、「繰り返し計算しても０から離れない点」に注目しました。
しかし、マンデルブロはむしろ「０から離れる点が、何度目の計算で離れていったか」に注目して、その回数を示したグラフを描きました。
一般的には、本来の（０から離れない）マンデルブロ集合を黒で、周囲の「数回の計算で離れた」場所を、計算回数に応じた色で塗り分けた図形となります。
色で表現する代わりに「高さ」として３Ｄ描画すると、険しい山に囲まれた湖のような画像となります。このような画像は、マンデルブロ湖と呼ばれます。
マンデルブロ集合もまた、ジュリア集合と同じような自己相似性を持ちます。
マンデルブロ集合は「ひょうたん型」をしていますが、湖（中央の黒い部分）の縁のあたりを拡大していくと、無数のひょうたんが見えてきます。
ひょうたんの周囲にはまたひょうたんが…コンピューターの計算精度の問題がなければ、無限に拡大し続けられます。
これは、計算中に「点」が中央付近を動き回り、無数の写像を作り出しているためです。
全体の写像が細部に現れるための自己相似性です。
（ただし、計算式は厳密な写像を作り出すものではないため、場所によって思わぬ形に変形します。これが余計に興味深い結果を生み出しています）
最初に挙げた問題提起ですが、「森の木々」は、1900年代初頭の試みでも描けるようになっています。
雲や蝶の羽の模様、燃え上がる炎の様子などは、マンデルブロの研究によって描けるようになりました。
他にも、現代の 3D CG や映画に使われる SFX などで、フラクタルの概念は欠かせないものになっています。
マンデルブロがフラクタルの研究を始めるきっかけとなった「株価の動き」ですが、こちらは「1/fゆらぎ」という現象名で知られています。
1990年代などに流行し、リラックスできる音楽とか、扇風機に「1/fゆらぎ」を名乗るものがありました。
自然界のいろいろな場所で1/fゆらぎが見られる、というのはマンデルブロの研究以前から知られていましたが、現代では「フラクタル」の一種としてとらえられています。
参考リンク：
気軽にマンデルブロ集合の描画を試せるサイトをリンクしておきます。
The Mandelbrot Set in HTML5 Canvas & JavaScript
昔、MSX2 のBASIC で、横256ドットの解像度で３日くらいつけっぱなしにして画面描画した覚えがあります。
X68k で「怪しい高速マンデルブロ」というプログラムがあり、機械語でテクニックを駆使して、１画面を10秒程度で描いていて驚きました。
今なら Javascript でも高解像度で一瞬です。
すごい時代だなぁ…
同じテーマの日記(最近の一覧)
関連ページ
ガストン・ジュリア 誕生日(1893)【日記 16/02/03】
別年同日の日記
申し訳ありませんが、現在意見投稿をできない状態にしています。 |
今日はジョン・ネイピアの命日（1617）。
生まれは1550年なのだけど、誕生日は不明。
ずっと以前に、歯車のページで「ネイピアの計算棒」として取り上げている道具を作った人です。
該当ページを書いたのは、今からもう１７年も前。
当時はこの道具のこともネイピアのことも知らず、科学館でやっていたイベントで見かけて面白かったので記事を書いた、と言う程度でした。
ネイピアは１６世紀の数学者…と過去には書いたのですが、当時の学者が皆そうであったように、貴族で領主でもありました。
そして、これも当時の学者としては当たり前なことに、占星術師で天文学者で物理学者でした。
そんなにたくさんの知識を持っていてすごい、と言うのではなく、当時はこれらの学問は切り分けられてなかったのですね。
占星術を行うには毎日の惑星の運行を記録してあることが大切だったので、天文の観察は必須でした。
たくさんの観察記録を元に、天体の動きを数式で解き明かす…やはり数学者で物理学者で占星術師のケプラーによって、天体の動きが解明されたのは1619年。ネイピアの死後のことです。
さらに、ケプラーの友人で、同じように占星術師で錬金術師でもあったアイザック・ニュートンが、天体の動きだけでなく万物に働く力としてまとめ上げ、後にニュートン力学と呼ばれる物理学の基礎を作り上げていきます。
…話が少し横道にそれましたが、当時は占星術や錬金術は重要な学問の一分野だったし、それを研究するのは決しておかしなことではなかったのです。
さて、話をネイピアに戻しましょう。
彼はなかなか良い領主だったようです。
肥料の改良などを研究し、彼の領土に住む農民に対し伝えたりしています。
また、外敵から領土を守るための軍事兵器の研究などもしています。
まぁ、領土を守るのは当然のことですし、税収を上げるためにも農業の改良は必要です。
そう考えると、領民のことを考えていたというよりは、彼の利益になるからそうしただけなのですが、ただ税率をあげて利益を搾り取るよりもずっと良いやり方です。
彼は、物事を単純化し、誰でも扱えるようにし、普遍化することに深い興味があったようです。
農業の改良も、一部の「頭の良い農民」「ベテランの農民」だけが多くの収穫を得られるだけではなく、その技術の普遍化を狙っていたのでしょう。
そして、これは彼の中心的な研究分野であった数学でも発揮されます。
難しい掛け算を、ただの足し算に変えてしまう魔法の道具。それが「ネイピアの計算棒」（ネイピアの骨、とも呼ばれます）でした。
彼の業績はこれにとどまりません。
彼の生きていた時代は、大航海時代でもあります。
そして、彼は占星術師でした。
この二つのことは無縁ではありません。
占星術師は星の観察が仕事ですし、船乗りたちは星を観測して現在位置を知ります。
星の観察で現在位置を求めるには、多くの桁数の数値を扱う必要がありました。
そして、計算を間違うことは遭難、死を意味します。
＃当時は小数点の考案前で、精度を上げる＝桁数を増やす、と言うことでした。
大きな桁数で計算したのちに、適当な母数で割ることで最終的な値を求めます。
ネイピア自身、天文学者で数学者ですから、大きな数との格闘の苦労は知っていました。
そこで、この大きな数を小さくしてしまう、という方法を考案します。
これが、対数の発見でした。
先に書いたようにまだ小数点は発見されていませんから、対数は整数の比（分数）で表されます。
現在の対数とはずいぶん異なりますが、大きな数を小さくするだけでなく、掛け算を足し算に変えてしまう（計算棒と同じように！）という、魔法のような方法でした。
先に、天文学者のケプラーの話を出しました。
ケプラーの師匠はティコ・ブラーエという人で、彼は膨大な惑星の位置の観察記録を残しています。
ケプラーは、この記録を元に運動法則を解き明かしました。
ネイピアは、対数があれば天体観測が簡単になる、というアイディアを、ティコに対して披露しています。
これが 1594年の話で、その時にはすでに対数のアイディアを持っていたことになります。
しかし、対数を扱いやすくするためには、あらかじめ対数を計算した「対数表」が必要でした。
この表を作るのが難事業で、対数の発表は20年後、1614年となっています。一般には、この年が「対数が発見された年」とされています。
その後、イギリスの数学者、ヘンリー・ブリッグスがネイピアと共に対数の研究を行い、改良がおこなわれます。
ネイピアの対数は独特の式によって分数で計算されたもので、今の対数のような「底」の概念などはありませんでした。
そして、表は分数で表現されていました。
これを、10 を底とした「常用対数」に改めます。10進法を使っている場合、この方が使いやすいためです。
ところが、これでは表を分数で表現しにくくなり、対数表の記述が難しくなります。
そこで…ここで初めて「小数点」と言う概念が考案されます。
先に、当時は小数点の考案前、と書きましたが、小数点はネイピア晩年の考案なのです。
ブリッグスは、老いたネイピアに変わり、常用対数表を完成させます。
しかし、完成はネイピアの死後でした。
ネイピアの計算棒は、掛け算を足し算に変えるものでしたが、足し算の計算は人間が行う必要がありました。
後にシッカルトが、足し算部分を自動化する機械を考案しますが、これは現存していません。
難しい技術を単純化し、普遍化するという意味では、シッカルトはネイピアの意思を継いだのでしょう。
そして、「計算を自動化する機械」は、現在ではコンピューターとして我々の手元にあります。
これもまた、ネイピアがいなくては作り出されなかった機械かもしれません。
対数分野では、常用対数より後に、非常に扱いやすい「自然対数」が考案されます。
自然対数は、常用対数以前にネイピアが考えていたオリジナルの対数の概念をさらに推し進めたものでした。
この自然対数の底 e = 2.71828.... は、現在ではネイピア数と呼ばれています。
計算尺はネイピアが考案したものではありませんが、対数の性質を利用して、掛け算を簡易に行うための道具です。
ネイピアの死の直後、1620年には原型となる「対数尺」が発明され、1632年にその後普及する物と同じ「計算尺」が作られています。
歯車計算機が作られた後も、計算尺には利点も多かったために1970年代まで使い続けられていました。
電子計算機の普及まで、350年も使われ続けた「計算機」だと言っていいでしょう。
そして、分数に変わる「小さな数を表現する方法」として考案された小数点は、現代では我々は何も意識せずに使っています。
10進数の延長上にあるためわかりやすく、小学校入学前の子供でも理解できます。
これもまた、ネイピアの考案によるものなのです。
同じテーマの日記(最近の一覧)
関連ページ
ジョン・ネイピア 命日(1617)【日記 15/04/04】
別年同日の日記
申し訳ありませんが、現在意見投稿をできない状態にしています。 |
今日はブレーズ・パスカルの誕生日(1623)。
うちのページ的には、パスカリーヌの開発者。
または、Pascal 言語に名を残す人。
「人間は考える葦である」という言葉で有名な哲学者ですが、パスカリーヌを考えたり世界初の公共交通機関を考案したりする発明家でもあり、確率論を創始した数学者でもあり、圧力の単位「パスカル」に名を残す物理学者でもあり、そして宗教家でもありました。
業績多すぎ。
それぞれ非常に興味深いものですが、本気で説明すると長すぎるのでざっと紹介。
興味を持ったら自分で調べてね。
パスカリーヌは別のページに書いてあるので簡単な概要だけ。
現存する、世界最古の「計算機」です。歯車で計算を行います。
現存しなくていいならもっと古いものもあるし、パスカリーヌは足し算・引き算しかできないけどね。
これ、当時のフランスの通貨体系が非常にややこしかったために作られた機械でした。
これ重要。そこをおさえとかないと、足し算引き算くらい機械を使わない方が速い、という話になっちゃう。
当時の通貨体系は「リーブル」。１リーブルは20スーで、１スーは12ドゥニエでした。
10進法と20進法と12進法が混ざってる。
普段の生活ならいざ知らず、税務官吏をやっていたパスカルのお父さんは、ややこしい体系に苦闘していました。
このお父さんの仕事をために、と発明した、なんと親思いの子供。ちなみに、17歳の時から製作を開始し、発明は19歳の時です。
確率論。
当時は賭博は非常に人気があり、当然必勝法は誰もが知りたいところ。
当然多くの人が同時多発的に確率論を研究しはじめ、パスカルもその一人に過ぎません。
しかし、彼は一人で研究を行ったのではなく、直感的に矛盾するような問題をいくつも考えては、友人を巻き込んで議論を始めたため、多くの数学者がこの問題を考えることになります。
あとで書きますが、パスカルは「自分で考える」ことを最重要だと思っていたようです。
だから、彼が研究して発表するのではなく、周囲に問題を投げかけて、考えに巻き込む。
巻き込まれた人が多く、パスカルの周辺で確率論の研究が進んだため、確率論はパスカルの創始、ということになっています。
以下は僕の個人的な話になりますが、大学１年の時に確率が必修でした。
しかし、その授業が厳しかった。単位を落とす人は珍しくなく、僕も例にもれず２回も落としました。
おかげで確率はそれなりに詳しくなり、あとでゲーム業界に入った際に役立ちました。
確率の使い方って、ゲームの面白さをかなり左右します。
せっかくいいアイディアなのに、ここら辺の処理でつまらなくなっているゲームもよく見ます。
圧力。
流体力学の原理の一つである「パスカルの原理」を見つけています。
油圧機器…パワーショベルとか、ダンプトラックとかは、パスカルの原理を応用することで非常に大きな力を出しています。
流体の圧力の研究をした功績から、圧力の単位に「パスカル」が使われています。
台風の中心気圧は 980ヘクトパスカル…とかいうときの「パスカル」ね。
これも僕個人の話を書くと、死んだ父は油圧機器の設計販売会社をやっていました。
別に父に教えられたわけではないですが、なんとなく油圧の原理とか好きでしたね。
ヘロンの噴水とかいつか取り上げたいテーマ、って、サイト作りはじめた 20年前から言っている気がする (^^;;
公共交通機関。
最初に書いたように、17世紀は富裕層と一般庶民の間には明らかな格差がありました。
富裕層の移動手段は馬車ですが、一般庶民は徒歩。
その時代に、パスカルは庶民でも安価に乗れる「乗合馬車」を考案し、実際に運用しています。
1662年に始められた乗合馬車は、世界初の公共交通機関とされています。
パリ市内の各地を結ぶもので、運賃は１区間５スー。
…先に説明しましたが、20スーが１リーブル。
事業の認可条件として「労働者は乗せない」などがあり、庶民でも上層を相手にした模様。
しかし、誰でも乗れるわけではないややこしい条件が嫌われ、思ったより利用が伸びず、採算があいません。
後に6スーに値上げしても厳しく、15年で廃止されています。
19世紀に入ってから乗合馬車は復活し、その際には「omunibus」と名乗ります。
「万人のために」という意味のラテン語ですが、略称として bus だけが使われたのが、現代の乗合自動車（バス）の名前の由来。
また、多くのものが相乗りをすることから、小さな話を寄せ集めて作る物語形式を「オムニバス」と呼びます。
人間は考える葦である。
パスカルは乗合馬車の運用開始から半年後に、39歳の若さで世を去ります。
元々病弱だったのですが、急に体調が悪化したのです。
死後、パスカルの考えを示すメモの断片が編集され、本として出版されます。
それが、哲学者としてのパスカルを有名にした「パンセ」でした。
「人間は考える葦である」はその中でも一番有名な言葉。
葦は弱い者の代表です。簡単に折り、殺すことができます。
人間の肉体はまた、簡単に死に至ります。その点では葦と同じ。
しかし、人間は考えることができます。思想はどこまでも自由です。
宇宙の果てを思うことも、遥かな未来を想うこともできます。
これが葦と人間の最大の違い。
ちなみに、「考えることは偉大だ」の後は、「愛はもっと偉大だ」と続きます。
考える、というのは所詮論理の積み重ね。論理なんて超えてすべてを包み込む愛はもっと偉大です。
さて、パスカルは宗教家でもあります。
16世紀にはじまった宗教改革は、宗教のあり方を変えました。
集金のための機関になっていた宗教のあり方を見直し、本来の宗教に戻そうとしたのです。
それでも、そこは宗教ですから、神の存在は疑う余地のない前提でした。
信じよ、さらば救われん。
ところがパスカルは、まず宗教を疑え、と問いかけます。
先に書いたように、宗教には集金機関の側面もありましたが、そうした部分は疑ったときにすぐぼろが出ます。
疑ってもやはり信じられる部分は、たぶん本物。そこを信仰すればよいのです。
さらには、神の存在を疑います。
パスカルは、研究テーマでもあった確率論を導入し、思考実験を行います。
その結果、神は存在しないかもしれないが、存在を信じて信仰することが、良い人生を過ごせるとの結論に達します。
これ、現代風に言えば「信念を持って生きる人は幸せだ」ってことです。
パスカルの時代には宗教が重要だったから「信仰せよ」となりますが、何か信じられるものを持つなら、何でもいい。
そして、信念を持っている人にとって、神がいるかどうかなんて些細なことなのです。
この言葉、先に書いた「愛は偉大だ」と呼応します。
本来ここでの愛は宗教用語（神の慈悲）なのですが、現代的に考えると「打算的ではない信念」…かな。
打算的ではない信念は全てを包み込むし、そういうものを持てる人は幸せな人生を送れる。
もっと簡単に言えば、趣味に打ち込める人はしあわせだ、ってことか。
これは卑近すぎるかもしれないけど、本質的に間違っていない気がする。
まぁ、現代でも十分に通じる、含蓄を持った言葉だとわかってもらえると良いです。
Pascal 言語。
これはパスカルの発明品じゃありませんね。名前の由来はパスカルですけど。
でも、もっとも僕のページらしい話題なので（笑）書いてしまいます。
ALGOL の影響下で作られたコンピューター言語で、そういう意味では C の親戚。
C は「高級言語のふりをしたアセンブラ」だと言われることが多いのですが、Pascal は本当に高級言語でした。
ここでいう「高級」というのは、ハードウェアの違いなどを気にしないで良い、という意味。
Pコードコンパイラとか説明したいけど、詳細に入り込み過ぎると長いので泣く泣く割愛。
Apple 社は、Pascal が好きでした。
Apple II 用にも Pascal の処理系を発売していましたし、Macintosh は Pascal の使用を前提とした ROM を持っていました。
Mac 発売後に C が流行して、Mac 用のプログラムは大抵 C で組まれることになります。
でも、内部 ROM の利用時には Pascal との互換性を気にする必要がありました。
文字列の持ち方とか、パラメータの積み方とか違うんだよね。
ちなみに、MacOS X に切り替えた際に Pascal とは決別したので、今は気にする必要ありません。
その昔、MS-DOS に TurboPascal という言語処理系がありました。
これ、優れもので、当時の遅い CPU でも一瞬でコンパイルが終わります。
それでいて、コンパイラ言語なので当時主流だった BASIC などよりずっと速いのです。
まるで魔法でした。
TurboPascal は後に言語仕様を拡張し、オブジェクト指向に対応しています。
しかし、これでは Pascal とは呼べないため、現在では Delphi という名前でリリースが続けられています。
昔ほどの人気は無くなってしまったようだけど、いまでもコンパイルの速さは健在で、気軽にプログラムを楽しめます。
そのため、趣味のプログラムをする人には人気があるようです。
同じテーマの日記(最近の一覧)
関連ページ
ブレーズ・パスカルの命日(1662)【日記 14/08/19】
別年同日の日記
申し訳ありませんが、現在意見投稿をできない状態にしています。 |
当ページ内では歯車計算機なんかも紹介しているのですが、その中に「ネイピアの計算棒」というものがあります。
これ、ページ開設当初（もう18年も前だ…）に、たまたま科学館で存在を知って書いたものです。
それほど詳しかったわけでもなく、ただ面白がって知ったばかりのことを書いただけなので、あまり深みが無い記事。
（今でも、書いている内容に深みなんてないけどさ）
＃ちなみに、その後知ったのですが「ネイピアの骨」と呼ばれることの方が多いようです。
いちいち計算棒のページを見に行かないでもいいように、概要だけ書いておきましょう。
計算棒は、掛け算九九が書かれた棒です。
この時、２桁の数字は、間に斜線が入っています。
上には、九九の「何の段」かが書かれていますので、この数字を並べて、掛けられる数を作ります（何桁でも良い）。
そして、掛ける数（こちらは１桁）の部分に書かれている数字を読み取ります。
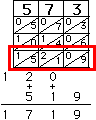
斜めの線により、隣同士の棒の数字が組み合わされます。
この数字を足して、書きだすと、答えがわかります。
たとえば、左の図では、573 * 3 = 1719 であることがわかります。
…言葉で説明するとややこしいな。
つまり、掛け算九九の表を使って、繰り上がった部分は上の桁に足していくと答えがわかるんです。
ただそれだけなのだけど、「掛け算」という結構大変な計算を、ただの足し算に変えてしまう道具です。
18年前にこの道具の紹介を書いた時は、「ネイピアの計算棒」の本当の価値がわかってませんでした。
これが、ネイピア数に名を残す数学者、ネイピアの作ったものであることがわかってなかったのです。
今日は、その数学者ネイピアさんの命日。
そして、ネイピア数とは、自然対数の底 e= 2.718281828459045235360287471352…
…いや、いいんです。
対数とか e とか、見ただけで嫌になる人が多いでしょうから、そんな話をしたいわけではない。
ネイピアは、対数を発見し、計算方法に革命を起こしました。
後にそのことが評価され、対数に関係の深い数字に、彼の名前が付けられたのです。
しかし、ネイピアが発見した対数は、現代的なものとは違いました。
ネイピアの時代には、小数の概念がまだ普及していなかったのです。
このため、できるだけ分数の比率で表しやすいように、対数の定義自体も異なっていました。
それでも、その「ネイピアの対数」は、現代の対数に通じる重要な特徴を持っていたのです。
対数の重要な性質とは…
なんと、対数を使うと、掛け算を足し算に変えることができます。
…ここでも、掛け算を足し算に変えようとしているのです。
ネイピアは、計算することの重要性を理解し、複雑な計算を誰でも簡単に行う方法を追求した数学者でした。
ネイピアの考案した対数を元に、後に計算尺が生み出されます。
計算尺とは、スライドする二つの棒を組み合わせた「計算機」です。
２つの棒には、対数で同じように目盛りがつけてあります。
ここで、
1) 棒 A の目盛り 1 の位置に、棒 B の「賭けられる数」の目盛りをあわせる。
2) 棒 A の「賭ける数」の位置の目盛りの下にある、棒 B の数を読み取る。
という簡単なことをするだけで、掛け算が終わっているのです。
棒をずらしたり、さらにずれたところにある数字を読む、という操作は、足し算に相当します。
これは普通の定規でも同じね。３の目盛りから、4つ離れたところの目盛りを読めば、７と書いてある。
ただ、計算尺では目盛りが対数で刻まれています。
そして、先に書いたように、対数では掛け算を足し算に変えることができます、
だから、足し算するような操作をすると、掛け算の答えが得られるのです。
より詳しく知りたい人は、こちらのページが詳細に書いてくれています。
是非、お読みください。
ところで、先ほどネイピアの時代には小数の概念が普及していなかった、と書きました。
それ以前は、小さな数は分数で表現しました。
しかし、ネイピアと同時代の数学者が、常に 10 の累乗を分母とする分数を使うと、整数部分の10進法と相性が良くて扱いやすい、と気づきます。
小数の概念の誕生です。
しかし、当初は表記法がスマートではなく、使いにくいものでした。
そこで、「小数点」を発案したのが、ネイピアでした。
これにより、ややこしかった「小さな数の表記」も簡単になります。
ここでも、ネイピアは「計算を簡単にしよう」と工夫を凝らしています。
現存する最古の歯車計算機であるパスカリーヌは、足し算と引き算しかできませんでした。
しかし、パスカリーヌの百年前に、シッカルトが歯車計算機を設計しています。
この機械では、なんと掛け算も可能でした。
その重要な仕掛けが、ネイピアの計算棒でした。
結局、歯車では足し算しかできないのですが、計算棒を使うことで掛け算を足し算に変換しているのです。
さらにいえば、現代のコンピューターでも同じ原理が活かされています。
表を使って掛け算を簡単な足し算に変換することで、高速な計算を行っています。
一方の計算尺は、電気化されて「アナログコンピューター」となります。
オペアンプ使って計算するのって、計算尺と原理的にそれほど変わるものではない。
でも、デジタルコンピューターが高速化するにしたがって、アナログコンピューターは消えちゃった。
コンピューターなんて高価だった時代、庶民は計算尺を使っていました。
でも、これも電卓が普及したら、やっぱ計算尺は消えちゃった。
でも、「対数の原理を使った計算方法」が消えても、対数の重要性は失われません。
むしろ、強力な計算機が使われるようになって、ますます対数の存在意義は増しています。
人間の知覚は、対数に従うようになっていることが多い、ということが知られています。
こうした、「人に合わせた感覚」をコンピューターで表現するには、対数の活用が欠かせないのです。
通常、オーディオ機器などの音量調節は、対数に従って音の強さを変えます。
対数に従った表示の時に、半分の位置に音量をあわせると、半分になったように感じるためです。
音楽を聴くときも、テレビを見るときも、現代ではコンピューターの応用機器になっています。
内部ではものすごい速度で計算が繰り返されていて、そこに「対数」が何度も顔を出しています。
ネイピアの計算棒はコンピューターの計算を裏で支える基本的な原理となり、ネイピアの発案した小数点と共に計算に使われています。
そして、ネイピアが発見した対数がその計算の中で繰り返し使われ、我々の生活をいたるところで支えてくれているのです。
追記？
書き終わってから気づいた。
去年も記事書いてるじゃんよ！
内容微妙に違うからリンクしときます。
同じテーマの日記(最近の一覧)
別年同日の日記
申し訳ありませんが、現在意見投稿をできない状態にしています。 |
今年の春ごろ…長男が5年生に進級したころだったと思うが、こんな質問をされた。
１～100までのすべての自然数で綺麗に割り切れる数って、どんな数だろう？
一応彼なりに答えは持っているのだけど、その答えが大きすぎて算出できない、という。
長男の考え方はこうだ。
まず、100 までの素数を探し出す。
100以下の数は、これらの素数を適切な回数掛け合わせることで作り出せるはずだ。
だけど、これらの素数を全て掛け合わせても、問題の答えにはならない。
素数をかけるだけでは、素数である「２」で割れることは保証されても、４で割れることを保証できない。
２を適切な回数掛け合わせることで、この保証を作り出さないといけない。
この「適切な回数」は、掛け合わせた数が 100を超えない最大の値になるようにする。
２であれば、６回掛け合わせて 64 にする。64 で割れる数字は、32、16、8、4、2でも割れることが保障される。
同じように、３ならば４回掛け合わせて 81とする。
全ての素数に対し、この操作を行う。
そして、最後にこれら掛け合わせて出来た数を、すべて掛け合わせる。
その答えが冒頭の質問の答えとなる。
説明を受けて、なるほど、と思った。考え方はあっている。つまり、それが答えだ。
でも、その数を実際に算出できない。
長男の疑問には条件に入っていなかったが、この数は、条件を満たすうちの「最小の数」でもある。
（素数を使った考え方は、最小公倍数の求め方と同じだ。
つまり、この数は１～１００の最小公倍数である）
この時点で、長男はためしに 10 までの数値で試算を行っていた。
1～10 の自然数で割り切れる数は、2520 だった。
その疑問は、大きすぎて解決できない数としてそのままになっていた。
夏休みも終わりに近づき、長男は宿題を全部終わらせ、急に「Scratch って、どのくらい大きな数を扱えるの？」と聞いてきた。
なかなか難しい質問だ。
宇宙物理学などで大きな数を使う時には浮動小数点を使う、という話は長男は知っているので、コンピューターも浮動小数点を使えることを教える。
その上で、Scratch 内部では 64bit 倍精度演算を行っていて、正確に出せるのは 52bit 分だけど、大きな数の表現としては、さらに 11bit 分の指数が付けられることを教えた。
ややこしい話に最初は混乱していたけど、次に「指数を使うと、大きな数は表現できるけど、その場合は細かな数は出ない？」と聞かれる。
うん、その認識で正しい。正確な数を求めたければ、52bit の範囲に収めないといけない。
じゃぁ、52bit ってどのくらい？ と聞かれたのだけど、即答できない。
32bit で40 億、さらに 20bit 余るけど、10bit で 1024 だから、40億の千倍の千倍くらい、と答える。
ここで、「じゃぁ、１～100までの全ての数で割り切れる数、計算できるかな」と言われる。
先に書いたように、冒頭の話は春のこと。僕はすっかり忘れていたけど、長男はまだ疑問に思っていた。
面白い、やってごらん、とノートパソコンの使用許可を出す。
＃長男が Scratch をやりたいときは、僕か妻に許可をもらってノートパソコンを借りている。
1～100までの素数は知っているのだけど、うまくいったらもっと大きな数も計算してみたいので、と、エラストテネスの篩から作りはじめる。
素数を求めるアルゴリズムね。プログラムの初心者向けの課題として良く出されます。
普通は配列で作るのだけど、Scratch には配列が無い。でも、リストがある。
最初にリストに 2～100の数字を入れて、「倍数」はリストから削除していく、というプログラムにした。
リストの先頭を取り出すと、それは常に素数。
素数を取りだしたら、リストの数値を順次確認し、取り出した素数で割った余りが 0 なら、削除する。
最後に、取り出した素数は、素数を入れるもう一つのリストに追加される。
元となるリストがどんどん削除されていくので、終わりに向かって加速していくプログラムが出来上がった。
見ていてなかなか楽しい。
これで素数が得られたら、次にそれらの素数を掛け合わせ、100を超えない最大の数にした数値を、また別のリストに入れていく。
最後に、リストに入った数値を全て掛け合わせれば答えが出る。
結果は… 6.9720375229..e+40 !
…残念！ Scratch では正確に求められないほど大きな数値だった。
＃最後が e+40 となっているのは、52bit の範囲を超えてしまい、指数表現になったことを意味する。
プログラムを作って、答えは出たけど、正確な数じゃなかったーーー と、残念がりながらも面白がる長男。
せっかくなので、ここは父の威厳の見せどころ。
自分のマシンに向かって、UBASIC を起動する。
というか、以前にちょっと使ってみようとしたけど、使い物にならなくてほったらかしてあったのね。
UBASIC は、DOS 時代のフリー BASIC 。
実効桁数なんと 8640bit (540word) という恐ろしい演算性能を持つ。
DOS では動いたけど、残念ながら今の Windows では動かない。
でも、フリーの DOS エミュレータである DOSBox 上では動く。
…のだけど、DOSBox は英語版 DOS だし、キーボードも US 101 キーボードが前提。
これが「使い物にならない」としていた理由。
とりあえず、数値演算だけだから日本語は使えなくてもいい。
エラーメッセージが文字化けして読めないけど気にしない。
長男の考え方を、どんどんプログラムしていく。
…のだけど、流石に US 101 キーボード用は使いづらい。
いちいち記号を探すことになって効率が悪い。
ちょっと調べると、改造品で 106 キーボード対応があったので、DOSBox を入れ替える。
後で書くけど、その後さらに環境整えたら日本語も出るようになった。
（この時は、BASIC プログラムを作ることが優先で、そこまでやってない）
久しぶりの UBASIC で無駄に手間取った部分もあるのだけど、2時間ほどで完成。
100 Max=100
110 dim F%(Max)
120 for I=2 to Max
130 if F%(I)=1 then 160
140 F%(P)=I:P=P+1
150 for J=I to Max step I:F%(J)=1:next
160 next
170 B=1
180 for I=0 to P-1:A=F%(I)
190 if A<Max/F%(I) then A=A*F%(I):goto 190
200 B=B*A
210 next
220 print B
BASIC ではリストは使えないので、素数を求める部分は普通の配列。
1だと「既にチェックされた」、つまり倍数であることを意味している。
＃ F% というのは、UBASIC 独特の書き方。1word 数値であることを示す。
0 か 1 かを保存するだけなので十分。
こうしないと、540word の変数を配列にしようとして、すぐにメモリ不足となる。
120～160 で素数を求める。
130 で倍数か素数か調べ、素数なら 140 で記録、150 で倍数をチェックしている。
170 からは素数が求まった後で、190 で「100を超えない最大の倍数」にして、200 行でそれを掛け合わせている。
長男が求めていた答えは 69720375229712477164533808935312303556800 だった。
後日追記 2015.9.7
こういう計算なら、UBASIC より Ruby がいいと思うよ、という重要な示唆をいただきました。
恥ずかしながら、Ruby に多倍長型があるのを知りませんでした。
Ruby で書き直してみたプログラムを含め、ここら辺の話、別の日記に書いています。
同じテーマの日記(最近の一覧)
関連ページ
別年同日の日記
申し訳ありませんが、現在意見投稿をできない状態にしています。 |
先日 UBASIC で 100 までの自然数の最小公倍数を求めた、という話を書いた。
そしたら、「ruby使えばいいのに」という重要な示唆をいただいた。
なるほど。調べてみると、ruby は UBASIC 以上の有効桁数で整数演算ができた。
僕は ruby 使いではないので知らなかった。教えてくださった方に感謝。
ruby は一度手を出したことがあったけど、勉強途中で頓挫したままになっていた。
手を出したのは、1999年。僕が会社勤めを辞めて独立した時だ。
当時は perl で WEB プログラムできる人材が求められていて、独立して perl プログラムで稼いでいた。
当時はネットが「新しいメディア」で、相場というものが存在していなかった。
学生がバイト気分で気軽に「プログラム書きます」なんて仕事を請け負っていたのだけど、生活が懸かっていないバイト気分なので、めっぽう安い。
でも、バイト気分なので責任感もない。金を払ったのに納期通りに上がってこず、催促しても「定期試験なんで」と仕事をしようとしない…なんて話も実際に聞いた。
で、そういう痛い目にあった人は、会社も設立して真剣に仕事を請け負っている、といえばそれなりの金額を出してくれた。
＃当時は今みたいに１円起業はできず、会社組織にしている、ということが本気度を示す指標だった。
でも、痛い目にあった人でないと、学生バイトと金額を比較され、同じとまでは言わないが安くやってくれないか、と値切り交渉をされる。
割に合わない仕事も何度かやった。
そして、じゃぁほかの人がなかなか手を出していない言語をやってみよう、と ruby に手を出した。
perl を勉強していたころから、perl をさらに使いやすくした言語として、ruby の噂は聞いていたから。
しかし、当時 ruby はそれほど有名ではない言語。上に書いたように、perl 使いの一部が気にしていた程度。
そんなわけで、ruby を勉強し始めてすぐに、ruby ができたところで仕事はない、と気づいた。
ちょうど仕事で知り合った人に「PHP を覚えてほしい」と頼まれ、PHP の勉強に切り替えた。
その人は日本PHPユーザー会の創設メンバーの一人だった。
当時は PHP だって知られておらず、覚えても仕事がありそうにはなかったのだけど、ありがたいことに PHP はその後有名になり、PHP ができるのであればそれなりに仕事があった。
さて、上に書いた話で ruby で勉強したのは、perl の延長として使えそうか、という程度の調査だけ。
プログラムを組むために、条件分岐や繰り返しなどの文法構造は理解したけど、データ構造を勉強する前に頓挫した形。
なので、bignum なんて存在を知らなかった。
＃1999年当時のバージョンでも bignum は存在したのかな…とネットで調査したところ、当時からちゃんとあったようだ。
だから、単に僕が勉強してなかっただけ。
この bignum 、なかなか優秀で、存在を全く意識する必要がない。
意識しないでよいからこそ、当時気づいていなかったのかもしれない。
下に、先日のプログラムと同等の計算を行うプログラムを示しておこう。
アルゴリズムなどは、ruby 向けに多少異なる。
Max = 100
F = Array.new(Max/2-2) {|i| i*2+3}
P = [2]
while a = F.shift
P.push(a)
F.reject! {|i| i%a==0 }
end
b=1
P.each do |num|
a=num
a*=num while a<=Max/num
b*=a
end
p b
大きく３つのブロックに分かれている。
最初のブロックは、準備を行っている。
最初の行で 100 と定義している。これで、100 までの自然数の最小公倍数を求める。
２行目では、3～100 までの奇数のリストを生成している。素数の候補だ。
３行目は、素数のリストの準備。唯一の偶数である２は、最初から入れてある。
中央のブロックで、エラストテネスのふるいを実行している。
奇数リストの先頭を取り出して、素数リストに入れる。
と同時に、reject を使って、奇数リストから、今取り出した素数の倍数を削除する。
最後のブロックでは、素数リストから順次値を取り出し、適切な倍率をかけ、b に掛け合わせていく。
最終的に b が最小公倍数だ。最後の行で表示している。
UBASIC では 6006 までしか計算できなかった。
6007 は素数で、それを掛け合わせると桁あふれしてしまうのだ。
しかし、ruby では 100000 でも計算できた。さすがに時間はかかるけど。
答えは、69528383... で始まる、 43452 桁の数値になった。
それはさておき、UBASIC インストール方法まで含めて書いたのは、実はそれなりの意図もあった。
まず一つ目は個人的な理由。
もともと計算は小学生の長男の興味で始まったので、長男に BASIC を教えようと思ったの。
特に書いてないけど、長男がエラストテネスのふるいを作る部分で悩んでいた時に、家にある初心者向けのテキストから、エラストテネスのふるいのサンプルプログラムを見せたのです。
でも、BASIC を理解していないと全く分からない。目の前にアルゴリズムの答えがあるのに、それが理解できない。
日本語環境まで整えたのは、長男に使わせたときに、エラーメッセージが文字化けするようでは扱えないためです。
でも、これだけなら家の中でやればよいことで、インストール方法まで明示する必要はない。
最近の言語は、グラフィックを扱うのにややこしい仕組みが必要なものが多い。
でも、BASIC 時代はグラフィックの扱いは簡単で、UBASIC も例外ではない。
そして、UBASIC では複素数演算ができる。
５年も前に「いつか書きたい」と宣言したまま一切書いていない、マンデルブロ集合の魅力について書くのに良いのではないか、と考えていた。
マンデルブロ集合って、非常に複雑で興味深い図形ね。
非常に複雑なのに、その図形を描くための方法は非常に単純。
Z = Z2 + C
という、たった一つの式を延々と計算し続けて、結果をグラフにすればよい。
ただし、Z も C も複素数、というのがみそ。たった一つの式ではあるけど、その式の意味が非常にややこしい。
当然のことながら、複素数の理解が必要。グラフとして示すので、複素数平面も知らなくてはならない。
さらに、一般の計算機言語では複素数を計算することができないため、実数部と虚数部を分離して計算するテクニックが必要になる。
画像の生成は非常に厄介だし、計算している座標系と、パソコン画面の座標系を変換するマッピングテクニックも必要となる。
UBASIC なら、複素数を計算できるし、グラフィックを簡単に扱える。座標系だって自由に変えられる。
なぜなら、UBASIC は高校生が数学に親しむために作られた言語だから。
「テクニック」が必要となる部分を、できるだけ言語側で吸収し、アルゴリズムの理解だけを求めるようになっている。
…と、熱い思いで語ったけど、実は先日以降実際にマンデルブロ集合を描くプログラムを作ったところ、あまりの遅さにどうしようか迷っている。
UBASIC でアルゴリズムの概要だけ示すけど、実行はお勧めしない、というような書き方になるかも。
ruby でも複素数演算パッケージは存在するようだし、これも ruby でやってもよいかもしれない。
こちらは、BASIC 程気軽にグラフィックを扱うことはできないようだけど、やはり描画パッケージ自体は存在する。
どちらにせよ、記事を書くとしたらだけどねー。
複素平面を理解してもらうためには、まず虚数の面白さから入らないといけなくて、そこで悩んでしまって書くのが止まっている。
一応、目標は「小学生でも理解できるようにしたい」ということなのだけど、虚数の必要性を伝えるのはなかなか難しい。
同じテーマの日記(最近の一覧)
関連ページ
別年同日の日記
申し訳ありませんが、現在意見投稿をできない状態にしています。 |
数学って、厳密で窮屈だと思っている人が多いです。
でも、数学ってものすごく「ファンタジー」な世界です。
SF小説がリアリティをもって「まだ見ぬ世界」を見せてくれるように、良質のファンタジーがおとぎの国を身近に感じさせてくれるように、数学は時として想像もつかない、面白い世界を見せてくれます。
良質の数学はファンタジーですが、確固とした理論の上に立っています。
良質のSF小説が、事実を組み合わせて、ありもしない世界を作り出すのと同じ。
たとえば、目の前に点があったとしましょう。
点があるにもかかわらず、大きさはありません。そんな点があるわけないのですが、ファンタジーですから。
これが「０次元」の世界です。
この点を２つ用意して、その間を線で結びます。「１次元」です。
線の両端を、点によって「囲んだ」ともいえます。
続いて、１次元の線４本で、空間を囲みます。
話を簡単にするために、角は全部同じ角度で、線の長さも全部同じだとしてください。
いわゆる真四角。正方形です。これは２次元。
正方形６つで、空間を囲みます。
今度は立方体。３次元。
ここでわかるのは、「次元が増えるごとに、空間を囲むのに必要な『１つ前の次元のもの』が、２つづつ増えていく」ことです。
１次元は、０次元の点２つで囲めます。
２次元は、１次元の線４つで囲めます。
３次元は、２次元の面６つで囲めます。
では、３次元の立方体８つで囲んだ空間を考えてみましょう。
…空中に浮かんだ十字架みたいな形、を思い浮かべるのは間違いですよ。
ここで、３次元の立方体８つのうち、隣り合うもの同士は「面」を完全に共有しています。
正方形の角は「点」を共有し、立方体の辺は「線」を共有しているように。
そんな形あり得ない？ ３次元ではね。
ここでは、「立方体」といいつつ、ひしゃげた形を想像してもいいでしょう。
ひしゃげているように見えて、実はひしゃげていない。
なぜなら、これは４次元の話で、３次元に住む我々には見ることができない図形だからです。
こうしてできた、立方体８つで囲まれた形を、「４次元超立方体」と呼びます。
この先はどういう形になっているのか想像もつきませんが、５次元、６次元の超立方体だって存在します。
超立方体！
形を想像することなんてできません。ただ、存在を受け入れてみましょう。
存在しえない、ファンタジーの世界です。
ネバーランドのお話を楽しむように。
中つ国、イーハトーブ、リリパット、ファンタージェン、ジーリー宇宙…それらの世界の物語を楽しむように。
…超立方体、というわけのわからない存在がある世界を、ただ受け入れて楽しんでみましょう。
でも、数学は確固とした理論の上に立っていますから、リアリズムのあるファンタジーです。
この超立方体にどういう特徴があるのか、論じることができるのです。
1970年にこんな問題が提起されました。
問題だけでもややこしいので、内容を３つに分けて書いていきます。
▼n次元の超立方体の、すべての頂点を、ほかのすべての頂点と線で結びます。
…想像できないでしょうから、普通の立方体、つまりは「箱」で考えてみましょう。これだって n=3 の超立方体です。
他の頂点と線で結ぶのですから、通常の「辺」に加え、各面に大きく「×」を書くことになります。
さらに、箱の内部にも、対角に当たる頂点まで「紐」を引っ張る形になります。
▼結んだ線は、２つの色のどちらかで描かれるとします。
先に想像した「線」は、すべて色がついているんです。
２色ですから、白と黒でいいでしょう。色の付け方はランダム、どのような形でも構いませんが、１本の線は１色です。
白黒といっても、縞模様の線があるわけではありません。
▼n が十分に大きければ、同一平面上の４点を結ぶ線がすべて同じ色になる組みが、必ず存在する。
前半は前提条件なので、後半から。
先に、立方体の場合、各面に×を描くことになる、としました。辺の部分もあわせると、面には６つの線が描かれます。
「同一平面上の４点を結ぶ線」というのは、そういうことです。
さらに、先ほど「箱の内部にも紐を…」と書きました。実は、この部分にも平面ができている。
超立方体だと、立方体よりもはるかに多くの面ができます。
そして、前半の前提条件。
「n が十分大きければ」です。
超立方体の次元が大きければ大きいほど、出来上がる面の数は多くなります。
それらの面は、別の面と辺などを共有しています。共有している、ということは、自由が利かないということです。
ですから、線の色を好きなように決めてよいとしても、すべてを思い通りにはできないのです。
そして、最後の結論です。
完全な自由が利かず、十分すぎるほど面の数も多いとき、面に描かれた６本の線の色が「すべて同じ色になる組みが、必ず存在する」のです。
問題提起は、単に「存在する」というだけでなくて、最小の n はいくつだろう？ というものです。
一応、問題の提案者は「少なくとも、n がこの大きさなら必ず存在する」という数を求め、証明して見せました。
そして、「それよりも小さな数になる n を探してくれ」と、世の中の数学者に問うたのです。
問題提案者は、今日が誕生日のロナルド・グラハム(1935)。
そして、問題提案時に示した n が、「意味のある数値として最も大きいもの」とギネスブックにも認定された、グラハム数です。
このグラハム数がまた、ファンタジーとしか言いようがありません。
話が壮大すぎて、誰もその数を計算できないのです。
33 …３の３乗、というのは、３を３回掛け合わせたもの、3*3*3 のことです。こうした計算を「累乗」と呼びます。
計算してみればわかりますが、 3*3 = 9 なので、3*3*3 = 9*3 = 27 。「3」という小さな数から急激に大きくなるのが累乗の特徴です。
コンピューター言語では、累乗を記号を使って表すことがあります。
BASIC では 3^3 、FORTRAN では 3**3 と書き表しました。
FORTRAN の書き方は、「掛け算の回数を掛け合わせた」という意味の書き方です。
「３の掛け算を３回行う」から 3**3 という書き方。
グラハムは、コンピューター関連の著書もある数学者で、こうした表記の意味をよく知っていました。
そして、BASIC 風の累乗の書き方を、FORTRAN 風の累乗の書き方によって「拡張」することにしたのです。
3^^3 という書き方は「３の累乗を３回行う」という書き方になります。
3^3^3 の意味で、計算手順としては 3^(3^3)。
先に書いたように、3^3 は 27 だから、3^27 の意味になります。
3*3*3*3* ... と、27回も掛け合わせると、答えは 7625597484987（７兆６千億）です。
3^3 の時も書きましたが、累乗は急激に数が大きくなります。
累乗には想像もつかない世界が待ち構えている。今回の話の重要なポイントになります。
さらに、3^^^3 という書き方もあります。これは、3^^(3^^3) を意味していて、3の累乗を 3^3^3 回重ねた数です。
この時点で、ものすごく巨大な数ですよ。3^^3 は先に書いたように７兆越えですから、3^3^3^3^3 …と、7兆回も繰り返すことになります。
この数、概数は計算されているけど、事実上計算できません。
素粒子１個で10進数１桁を表すことができたとして、現在見積もられている「全宇宙」の素粒子を使っても、この数を表記できないくらい大きいそうです。
さて、 3^^^3 とか 3^^^^^^^^^^3 とか、記号が増えすぎると記号の個数を数えるのも大変になるので、別の書き方をしましょう。
3^^3 のことを、G(2) と書くことにします。G はグラハムの G ね。
G(3) なら 3^^^3 のこと。G(4) なら、3^^^^3 のこと。
さっき、G(3) でもすごく巨大な数だ、と書きました。
G(4) になると概数の計算すらできていません。
そしてもうひとつ、ルールを追加します。
G2(4) とかいたら、G(G(4)) のことです。
G3(4) なら G(G(G(4))) のこと。
では、G64(4) と書いたら？
話が壮大すぎてついていけません。
数学が苦手だからわからない、とかではないよ。
数学者であっても、誰もこの数がどのくらいの大きさか理解できていません。
これが、グラハムが冒頭にあげた「n が十分大きい超立方体の各頂点を結ぶ線を２色で描いたときに、面を構成する線がすべて同じ色である面が必ず存在する」という証明に使われた、次元の数です。
n が G64(4) よりも大きいときには必ず成り立つ、という証明はできました。
だれか、もっと小さな数でもできると証明してくれ、というのが、グラハムの出した問題なのです。
この G64(4) のことを、「グラハム数」と呼びます。
先に書いた通り、意味のある数値として一番大きい、とギネスブックに認定されています(1980)。
その後、問題を満たす小さい数として「小グラハム数」が見つかったけど、これも十分に大きな数でした。
グラハム数に比べれば、ずっとずっと小さいのだけどね。
逆に、n が 6 未満では問題を満たすことができない、という「下限探し」の証明も提出されています。
現在、6ではちょっと小さすぎて、11 よりも大きいのではないか、とされているようです。
同じテーマの日記(最近の一覧)
別年同日の日記
02年 Synchronized, wait & notify
申し訳ありませんが、現在意見投稿をできない状態にしています。 |
今日は、ガストン・ジュリアの誕生日(1893)。
添付している画像は、節分なので鬼のお面…ではなくて、今日紹介するジュリアが考案した、ジュリア集合図形の一種。
この複雑な図形、たった一つの数式で描かれている。
描き方は後で紹介しよう。
ジュリアは19世紀末に生まれた、20世紀初頭の数学者だ。
19世紀の数学は、微分・積分を究極の武器として発達した。
20世紀初頭には「違う方法での数学アプローチ」が求め始められていて、あらゆる部分で微分「不可能」な図形が多数考案されたりしている。
微分とか積分とか聞くと拒否反応を示す人もいるので、簡単に説明しよう。
微分可能、というのは、言い換えれば「滑らかだ」と言っているだけだ。
微分すると、結果としてその「滑らかさ」の度合いを知ることができる。
でも、ここでは結果はどうでもいい。可能かどうかだけを聞いているのだから。
これは、「滑らかか」と聞かれているだけだ。
直線はどこまでもまっすぐで、滑らかだ。円周もどこまでも滑らかだ。
これらは微分可能だ。
でも、三角形の角は滑らかではない。ここを「微分不可能な点」と言ったりする。
じゃぁ、あらゆる部分で微分不可能、とはどういうものだろう。
多くの数学者は、「線」の定義を変えることで微分を不可能にした。
コッホは、直線の定義を「２点の間を３分割して、両端は直線に、中央は三角形の残りの二辺の直線を描く線」と定義しなおした。
…おっと、ここで注意しなくてはならない。コッホは直線を定義したはずなのに、その定義の中に直線が入っている。
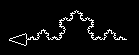この定義には「分割」が入っている。定義の中に定義自身が入ることで、無限に分割され、無限の「三角形の角」を生み出す。
先に書いたように、三角形の角は微分不可能だ。
そのため、コッホの考案した、この「コッホ曲線」は、あらゆるところで微分不可能となる。
19世紀の数学は、微分・積分を究極の武器とした。
その事実から考えると、「あらゆるところで微分不可能」というのは、非常に恐ろしく、非常に興味深い図形だ。
ジュリアは、ここに虚数を組み合わせた図形を考案した。
虚数！
…あぁ、また「難しそう」と思う人がいそう。
この際、虚数の計算方法はどうでもいい。これが興味深いものであることだけを示そう。
普通の数は、「数直線」の上に表すことができる。小学校で習うね。
同じように虚数も、虚数の数直線の上に表すことができる。この点では、普通の数と何も変わらない。
ただ一つ違うのは、虚数の数直線は、普通の数直線と「直角に」交わっている、ということだ。
この世界に、虚数は存在しない。数学者の頭の中だけに存在する、と言われる。
実は、物理学的にも虚数は存在していると考えたほうが都合がよい…つまりは、実際にも存在しているのだけど、少なくとも我々の誰も、その虚数を感じ取ることはできない。
たとえ、虚数の「計算方法」を知っている物理学者であったって、その存在を実感することはできないんだ。
なんでかというと、我々は数直線に落ちた「影」を見ているから。
数直線の上にある、と思われている数は、実は数直線の上ではなく、自由な位置にある。
ただ、その位置から数直線に向けて、まっすぐに「影」を落としている。そして、我々はこの影しか見ることができない。
だから、世界に虚数があったとしても、誰一人として感じ取ることはできない。
さて、数が自由な位置にあり、数直線に影を落としているだけだとしたら、本当の数はどこにあるのだろう？
先に書いたように、虚数は普通の数と直角に交わったもの、と考えることができる。
となると、自由な位置にある…普通の数だけでは表現できない数も、虚数を組み合わせれば表現できる。
これが、「複素数」と呼ばれるものだ。
普通の数と虚数の、二つの数直線を使って「平面」を示すとき、これは複素数平面と呼ばれる。
混乱しないように書いておくと、普通の平面なら、(X,Y) の二つの数字で点を示すことができる。
複素数平面は、 X が普通の数で、 Y が虚数だというだけ。これ自体特別なものではない。
ジュリアの研究は、この複素数の奇妙な性質を調べるものだった。
先に複素数を「自由な位置にある数」と呼んだ。
複素数自体は、普通の数と虚数の組み合わせで示されるけど、決して二つの数ではなく、これで一つの数だ。
１つの数なので、計算ができる。
そこで、こんなことを考えてみよう。
1) 複素数 z に対して、最初の位置 z0 を与える。
2) z に対し一定の操作をしたうえで、複素数 c を足す。
3) 2 でできたものを新たな z として、何度も 2 を繰り返す。
4) 発散したかどうかを、z0 の位置ごとに記録する。z0 を変えながらひたすら繰り返す。
「一定の操作」というのがわかりにくいのだけど、自乗とか３乗とかが一般的だ。
なんでもいいのだけど、「一般的」なものは、面白い挙動が見られるからよくつかわれる（一般的である）。
複素数 c も、なんでもいい。ただし、これは一連の計算の間は固定の値だ。
で、一連の計算というのは、 3 でひたすら繰り返すし、4 で 1 の条件を変えながらひたすら繰り返す。
ものすごい数の計算をしなくてはならない。
4 で「発散したかどうか」とあるのだけど、ここは注意深い説明が必要だ。
なぜなら、ここに複素数の奇妙で興味深い振る舞いが現れるから。
普通の数…まぁ、整数としておこう。整数なら、自乗すれば大きくなる。何度も繰り返せばどんどん大きくなる。
0～1 の範囲の数だと、何度も自乗すれば小さくなる。今度はどんどん小さくなる。
どちらにしても、どんどん一つの方向に向かって数が動き続ける。
でも、複素数はそうじゃない。虚数は、自乗すると「マイナスの数になる」という性質があるからだ。
計算方法はややこしいので書かないけど、大きくなろうとする普通の数と、それを引き戻そうとするマイナスの数がせめぎあって、あちこちを行ったり来たりすることになる。
さらに、複素数 c を足しているので、この振る舞いは非常に興味深いことになる。
ただ、ある程度複素平面の原点 (0,0) から離れすぎてしまうと、すごい勢いでどこかに飛んで行ってしまうことはわかっていた。
数学的には、すごい勢いで数が離れていくことを「発散した」という。なので、原点から離れると発散する。
ジュリアは、この「興味深い」動きを調べようとした。
z0 を少しづつ変えながら、発散したかどうかを記録し続けた。
先に書いたように、ものすごい数の計算が必要だ。
ジュリアの時代には、手回し計算機があったので、手で計算していた時代に比べれば高速に計算できたから、こんな手間のかかることをやろうとしたのだろう。
とはいえ、現代の…コンピューターの計算力を知っている我々から見ると、なんとも気の遠くなる作業だ。
結果は、非常に興味深い。最初に与える z0 が原点に近ければ発散しない、というような単純なものではない。
発散した点とそうでない点を塗り分けると、非常に複雑な図形が出現する。
そして、その境界は非常に微妙だ。
発散した点だらけのあたりで適当に取った点は、やはり発散する。
発散しない点だらけのあたりだと、やはり発散しない。
でも、境界線当たりでは、ほんのわずかに数値を動かしただけで、挙動が変わってしまう。
つまり、「どんなに細かく見ても、境界線を見極められない」。
これこそ、すべての点で微分不可能である、という、最初に書いた図形の一種なのだ。
おそらくジュリアは、複素数の興味深い振る舞いを調べたかったのだろうけど、20世紀初頭に流行した図形のバリエーションを…非常に独創的な方法で作り出したことになる。
ちなみに、最初に示した「鬼の面のような画像」は、 z^2 * exp(z) + 0.21 、という操作で作られている、そうだ。
Wikipedia で CC BY-SA 3.0 ライセンスのものを、ライセンスに従って使わせてもらった。
本来のジュリア集合は、この図の「黒い部分」である。
発散してしまった場合、発散するまでの計算回数を元に、点に色を付ける。
すると、美しいグラデーションが現れる。近い点は、同じ程度の計算回数で発散しやすいためだ。
しかし、見てわかるように、単純なグラデーションとはならない分断面も多数ある。
こうした複雑さがジュリア集合の面白さになっている。
ジュリアの時代には、計算力が足りなかった。
ジュリアは方法論を示して後の世に影響を与えたけど、時代が早すぎた。
ずっと後の話になるのだけど、マンデルブロがこの「ジュリア集合」に興味を示す。
その時にはコンピューターがあったので、簡単に計算を行うことができた。
先に書いた通り、ジュリア集合は原点 (0,0) 付近を離れない点の集合だ。
関係するパラメーターはいくつもあるのだけど、計算するごとに足し続ける値、c は非常に重要になる。
この c の値によっては、初期値が原点の場合ですら発散してしまうことがある。
そこで、マンデルブロはまず、ジュリア集合世界の「見取り図」を作ろうとした。
まず、計算を単純な「自乗」だけに限定した。
初期値 z0 を、原点である (0,0) にして、c の値を変えながら、ジュリア集合と同じように繰り返し計算を行った。
そして、c の位置に応じて、発散したかどうかを複素平面に描いていく。
マンデルブロの目的は、「興味深い振る舞いをしそうな c の値」を探し出すことだった。
原点ですらあっという間に発散するようでは、その c の値に見どころはないからね。
しかし、この「見取り図」こそが、ジュリア集合以上に興味深いものだった。
見取り図を作ることが目的だったので、ジュリア集合よりもずっとパラメーターが少ない。
にもかかわらず、ジュリア集合と非常によく似た振る舞いを示し、細かな部分にジュリア集合と類似のパターンが現れた。
マンデルブロが作成した「見取り図」を、マンデルブロ集合と呼ぶ。
今となっては、マンデルブロ集合はジュリア集合以上に有名だ。
ジュリア集合、マンデルブロ集合、を含み、先に書いたコッホ曲線など、「微分不可能な数学」の一分野を、マンデルブロは「フラクタル幾何学」と名付けた。
今では、このフラクタルの概念も拡張され、いろいろなところで役立っている。
そう、なんだか難しい話に思えた人も多いと思うけど、身の回りで役に立てられている技術だ。
マンデルブロとその業績については、マンデルブロの命日の記事に書いているので、興味がある人はそちら読んでほしい。
同じテーマの日記(最近の一覧)
別年同日の日記
申し訳ありませんが、現在意見投稿をできない状態にしています。 |
このタイトル、すでに分からない人の方が多そうだな。
急に思い出話。
まだ僕が大学１年生だったころのこと。
PCルームがあって、放課後は入り浸っていた。
その場にいる人の多くは、僕も所属していたコンピューターサークルのメンバー。
でも、そうではない常連の人もいて、学科もサークルも違うのに知人、という人もいた。
そのうちの一人…同じく１年生で、簡単なプログラムは組めるが本格的なゲームなどは作れない、というくらいの知人が、ゲームによくある、ジャンプの動きを作ろうと頑張っていた。
その知人は「ジャンプは放物線なのだから」と、何かの二乗を使って書こうとしてたんだ。
（二乗のグラフとして描かれる線を、放物線と呼ぶ）
でも、そうじゃない。ゲームならジャンプは次のように書く。
（当時は BASIC を使っていたので、BASIC 風に）
10 X=X+1
20 IF INKEY$=" " THEN JUMP=1:Y1=-5
30 IF JUMP=1 THEN Y=Y+Y1:Y1=Y1+1
40 IF Y1>5 THEN JUMP=0
50 PUT SPRITE 0,(X,Y),8,0
60 GOTO 10
このプログラムはサンプルなので、初期設定を省いているので、雰囲気で読んで欲しい。
ともかく、こんな感じのプログラムを作って、こうやるんだよ、と見せてあげた。
そうしたら、返ってきた反応は、「なんかずるい」だったんだ。
動きを見ると放物線っぽく見えるけど、プログラム中には二乗どころか、掛け算もない。
それは放物線ではない、というのだ。
いや、別にずるくないよ、と言い返したが、その時の自分には「ずる」ではないという明確な根拠を示せなかった。
今なら明確に示せる。
これは、放物線の式に対し、一階微分した導関数を導き出し、その導関数を再び積分することで放物線を再構築しているんだ。
なぜ微分するかというと、ゲームは時間によって微分された世界で動いているから。
テレビ画面は、連続した「時間」を、1/60 秒ごとに区切って表示する。
このわずかな時間の動きは、時間で微分されている、ということになる。
そして、その微分したものを積み重ねていく。
テレビで言えば、一連の「コマ」を連続させて動かすことが、積分にあたる。
…厳密にいえば、微分ではなく差分だし、積分ではなく積算なのだけど。
これを言い出すと離散数学というややこしい数学の話になるので、今は微分積分という呼び名で話を進める。
僕のプログラムを見た知人は、「プログラム中に二乗がないので、放物線ではない」と言った。
しかし、プログラム上は微分したことで二乗が消えている。
そして、プログラムを動かすと時間変化によって積分され、正しい放物線が描かれる。
これを「ずる」だというのは、微分積分を理解していない残念な人間だというのを、自ら明かしたに過ぎない。
（もっとも、すぐに言い返せなかった自分も、その時には十分理解できていなかったわけだけど）
本当に足し算だけで二乗になるのか、まだ疑う人がいるかもしれないので、わかりやすい例を挙げよう。
まずは、単純なルールで作りだせる、次の数値の表を示そう。
| 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 |
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 |
この表のルールはこうだ。
・上に書かれた数値は、その左側の列の上下の数値を足したもの。
・下に書かれた数値は、その左側の列の下の数値に、2を足したもの。
足し算しか使っていない、非常に単純なルールだ。
おかしいところがないか検算してもらってもよい。
ここで、上の数値は、もう一つの意味を持つ。
0,1,2…と続く数値の「二乗」になっているのだ。
日本人なら 9*9=81 まではわかるだろうから、上の表は 81 で止めてある。
でも、もっと長く続けても大丈夫。これも試してもらってよい。
「ずる」と言われたのが悔しくて、根拠を考えていたら、数日後にはこの答えに行きついた。
でも、サークルも違うし学科も違ったので会う機会はそれほどなく、言い返すタイミングは永久に失われた。
それを思い出して急にここに書いたのは、ネットで「微分積分なんて実生活でどう役に立つのか」なんていう…まぁ、よくありがちな学生の愚痴を見たから。
微分積分、生活で超役立つ。
上に書いたように、テレビゲームは微分積分の世界の中にある。
そもそもテレビが微分積分の世界だし、デジタルテレビなんかフーリエ変換（微分積分の親玉みたいなやつ）を駆使して作られている。
ただし、役立てられるかどうかは、自分次第。
ゲームやテレビの中に微分積分が駆使されている、なんていうのは知らない人は全く気付かない世界だ。
それでも生活はできるのだから、知らずに生活している限りは、高校で習った微分積分は「役立てられていない」。
役に立たないのではなく、役立てられないのだ。
なんでかといえば、勉強が浅かったから。「どうせ役立たない」なんて思ってるから。
世界最初のコンピューター、と呼ばれる ENIAC は、実のところ「ひたすら足し算する機械」にすぎない。
それでも、数学的に正しい…どころか、空気抵抗なども考慮した「弾道計算」ができた。
先に書いたように、足し算だけで数学的に正しい放物線は求まる。
しかし、それは空気抵抗や風などがない理想状態での弾道にすぎない。
ENIAC では時間で「微分」した方程式を使い、繰り返し計算して「積分」することで、弾の速度の関数となる空気抵抗や、風の影響なども考慮に入れ、物理現象としての「弾道」を描き出すことができた。
空気抵抗が弾の速度の関数になる、なんていうのは、瞬間ごとの速度を見ながら抵抗を導き、それによって速度を調整する、というのを繰り返しながら積分する方法でないと計算できない。
そうした計算が複雑すぎて人の手に負えないから、ENIAC を建造したわけだけど。
ともかく、ここで重要なのは、どんなに複雑な数式であっても、微分を繰り返せばただの足し算になるということだ。
そして、足し算をひたすら繰り返せば、元の複雑な数式の答えを導き出せる。
（ここでいう答えとは数値演算であり、式の変形ではない）
ENIAC は弾道計算よりももっと複雑な、水爆の内部圧力の計算なども行っている。
使われた計算は全部足し算のみだ。それが微分積分の威力だ。
今回、この話を書こうと思ってネットを調べていたら、以下のようなことを書いている人がいた。
（一連のツイートだが、特定人物を批判したいわけではないため、検索されないよう文面は変えている。）
・ファミコンで三角関数を使うと遅くなるので、スーパーマリオのジャンプは掛け算だけで作られている。
・掛け算だけなので本当は放物線ではないのだが、ゲームを作るうえでのうまいごまかし方だと言える
…まぁ、プログラマーでない人がうろ覚えの知識を披露しただけだと思う。
しかし、どこから突っ込んでよいかわからないほど違っている。
まず、ジャンプを表現する放物線に、三角関数は必要ない。掛け算だけでよい。
そして、ファミコンは掛け算すら遅いので、足し算だけで作られている。
さらにいえば、先に書いたように足し算だけで書いてもごまかしではなく、数学的に正しい放物線が描ける。
ただ、スーパーマリオのジャンプは、放物線ですらない。
放物線にすると、操作が難しくてゲームにならないから。
それでも放物線っぽく感じられるようにしている。
これが「うまいごまかし方」だというのは同意だが、計算できなかったからではなく、ゲームを面白くするためだ。
背景が全く違う。
同じテーマの日記(最近の一覧)
関連ページ
別年同日の日記
申し訳ありませんが、現在意見投稿をできない状態にしています。 |
少し前の日記で、微分積分は役立つよー と書いたのだけど、話の腰を折るのであまり具体例に踏み込まなかった。
これ、自分の中で気になっていて、もう少し説明したいと思っていた。
僕はプログラマーなので、これから書くのはコンピュータープログラムとしての微分積分の話だ。
そして、プログラムとしての微分積分というのは、高校で習ったアレは何だったのかと気が抜けるほど簡単だ。
まぁ、高校で習ったことはちゃんと意味があるので、そのフォローは最後にやる。
▼積分の概念
というわけで、微分積分の「考え方」から説明しよう。
微分積分、と言っているとややこしいので、まずは積分に話を絞る。
前提知識として、足し算は理解しているものとする。
足し算がわからない人には、さすがに説明ができない。
では、[ 3, 3, 3, 3 ] …3 が４つあるのだけど、全部足してみて欲しい。
答えは 12 だ。3 + 3 + 3 + 3 でいいのだけど、3 × 4 と考えるとすぐに答えが出る。
次に、[ 3, 4, 5, 6 ] を全部足してみて欲しい。
今度は掛け算は使えないので、地道に足し算をするしかない。
3 + 4 + 5 + 6 で、答えは 18だ。
概念的には、後者が積分にあたる。
たくさんの数をまとめて足す方法が積分。
そのうち、数が「たまたま全部同じだった」という特殊な場合が掛け算だ。
ここに書いた例では、４つの数を足しただけだった。
これが、数万という数があると考えて欲しい。とても手計算で足し合わせることはできない。
でも、それらの数に何らかの法則があって、数式で表せたとしよう。
こうなると話が変わってくる。足したい数の概要を数式として示せたので、これをもとに「全部足した結果」の数式を作り出す。
すると、数万件の足し算をする必要がなくなり、すぐに答えが出る。
これが、高校で習う積分だ。
ただ、数式で表すとなると、整数だけが相手というわけにはいかない。
式を変形するための前提条件などもいろいろと付き、話が複雑になっていく。
結果として「難しい」と思われてしまうのだけど、やりたいことは「全部足す」なのだ。
さて、そこでコンピューターが開発された。
最初は、「ひたすら足し算」しかできない機械だった。
でも、足し算さえできれば積分計算ができる。それで十分だ。
今のコンピューターもその延長上にあるので、プログラムのいたる所に積分が顔を出す。
多分、多くのプログラマーが、積分だとも思わないまま使っているのだけど。
▼積分の具体例
具体例をあげよう。
最近の家庭用テレビゲーム機では、コントローラーを振って操作することができる。
３Ｄのゲームで、コントローラーを左右にふることで、左右を見ることができたりね。
これ、コントローラーには「向き」を知るための仕組みは入っていない。
入っているのは、加速度センサーだ。
加速度、というのが馴染みが薄いかもしれないのだけど、単純に力のことだ。
加速度センサーは、コントローラーにかかる力を知ることができる。
そして、速度に加える、という名前の通り、足し算を続けると…つまり、ここまでに説明したように「積分」すると、現在の速度が得られる。
さらに、速度を積分すると、今度は現在の位置が得られる。
自分の体を中心としたコントローラーの位置と考えると、「向き」と近似のものだ。
こうして、加速度センサーから得られる値を、2回積分することで、コントローラーからは直接得られない「向き」を算出しているんだ。
積分を行うと、値のもつ「意味」を変えることができる。
ここでは、加速度を速度に、速度を位置に、変えることができた。
長さを面積に、更に体積に変えることもできる。
掛け算でも同じだけど、先に書いたように、掛け算は積分の特殊な場合だから。
プログラムしていて、欲しい値が手に入らない、ということはよくある。
そうした場合でも、手元にある値を積分することで、欲しい値を作り出す事ができる。
プログラマーなら、こうしたプログラムの経験はいくらでもあるだろう。
積分というのは特別なことではなく、ごく当たり前に使われるものなのだ。
また別の例を上げる。
積分を使うと、複雑なものを単純化できる。
物を投げたときの位置は、それほど難しくない数式で示すことができる。
いわゆる放物線だ。
まぁ、人がボールを投げるくらいなら放物線の式で問題ない。
でも、高速で動く場合は空気抵抗が問題になり始める。
そこまで考慮して位置を示す式を作ろうとしても、複雑すぎて作ることができない。
そこで積分を使う。
いきなり位置を表す式を作るのではなく、まず速度の式を作るのだ。
空気抵抗は速度によって変わるので、速度をもとに空気抵抗を求め、その空気抵抗で速度が変わるようにする。
そして、その速度を積分して位置を求める。
ここで言う積分は、もちろんコンピューターの計算力で足し算を繰り返すことだ。
このように、複数の段階に分けることで、複雑すぎて手に負えない計算も行うことができる。
こちらも、プログラマーにとってはそれほど特別なことではないね。
ゲームを作る人なら、いろいろな条件で途中から動きが変わったりする、つまり「加速度」を持つプログラムは当たり前に組むだろう。
▼微分
積分の話を2つほど挙げたが、続いて微分のことを書こう。
微分は積分の逆の操作だ、と思ってだいたい間違いはない。
微分して積分したらもとに戻る。
積分がすべて足すのに対して、微分は直近の値を引く。
これによって、直近から値がどのように変わったのか、その「差」を調べることができる。
積分例として、ゲームコントローラーの話を書いた。
コントローラーには加速度センサーしか入っていないが、積分すれば位置がわかる。
逆の話として、スマホのタッチパネルのことを書こう。
タッチパネルに指を触れると、その位置がわかる。でも、位置以外はわからない。
しかし、タッチパネル操作でスクロールを行うとき、「フリック」すると、その時の速度でスクロールが続く。
ここでは、指の位置情報を微分することで、速度を求めているんだ。
フリックとは、指を動かしている最中に、急にタッチパネルから離す動作。
指が離れた直前の速度がある程度あった場合、そのままスクロールを続けるようにする。
そして、徐々にスクロールが止まるのは、速度を変化させる、逆向きの加速度を設定している。
これらの動作は、積分を行っている。
微分すると、変化がわかる。
これを多用しているのが、写真などの加工アプリだ。
ある点に注目したときに、すぐ隣の点との差を出す。
これを画像のすべての点について行い、その結果を新たな画像とする。
これが「画像を微分する」ということなのだけど、この結果得られるのは、色の変化するところを拾い出したような画像だ。
いわゆる「輪郭抽出フィルタ」だと思っていい。表示の方法によっては、レリーフ化フィルタになる。
この輪郭に対してもう一度微分すると、輪郭のすぐ隣の点を際立たせるデータが得られる。
これを元の画像に重ねると、輪郭がくっきりとする。
「シャープフィルタ」とか「ピンぼけ補正フィルタ」と呼ばれるものだ。
ここに書いたのは単純な原理だけで、実際の画像処理ではもっと工夫された処理が使われている。
しかし、微分の応用範囲の広さはわかってもらえると思う。
▼微分積分とは
これ以上書いても同じような話ばかりになりそうなので、少し話を変えよう。
微分積分というのは難しいものだ、と思っている人は多そうだ。
でも、コンピューターで計算するときは、ただの足し算引き算だ。
特に難しい処理ではない。
じゃぁ、なんで高校ではあんなにややこしい教え方するのさ、という話。
これにはもちろん意味がある。
微分積分学は19世紀に大きく発展したのだけど、コンピューターの登場は 20世紀なのだ。
だから、学問としてはコンピューターのほうが新しく、難しい。
高校でやるのは積分の「基礎」で、コンピューターを使うのは「応用」なのだ。
今回書いた話も、概念としては「微分積分」なのだけど、数学的な妥当性はちょっと怪しい。
わざと簡単な話だけやっていて、ややこしい話は避けたからね。
真面目に書こうとすると、高校レベルの数学では収まらない話になる。
でも、今回僕が示したかったのは、数学的な妥当性ではない。
難しいと思って避けている人が多い「微分積分」が、案外身近に使われているし、考え方自体は簡単なものだと知ってほしかったのだ。
▼最後に
微分積分の話、もっと書きたいことはたくさんある。
でも、何でもかんでも盛り込むと話が横道にそれ過ぎて、わかりづらくなる。
今回も、これでも泣く泣く削った話が多数あるのだ。
諦めきれないネタを２つ、概要だけ示す。
説明は長くなるからしない。書きたいから書きっぱなしにする、というだけ。
・太陽の位置と季節の話
12月の冬至と6月の夏至が「昼と夜の長さ」のピークなのに、寒さと暑さのピークは2月と8月だ。
なんでピークがずれるのか気になったことはないだろうか？
太陽の運動を正弦波、太陽エネルギーを気温に変えるのに積分が必要だと考えると、大体理解できる。
・フーリエ変換
異世界転移の魔法。
ネイピア数を虚数乗することで複素空間に円形の魔法陣を描き、そこに波動をぶつけて積分すると「周波数空間」という異世界に転移できる。
もちろん、異世界に行ったら無双できるのがお約束。
…と、与太話を書いてから真面目に解説したかったのだけど、そもそもこの与太話がフーリエ変換を理解していないとわからないし、解説もすげー長くなるからやめた。
同じテーマの日記(最近の一覧)
関連ページ
別年同日の日記
17年 タネンバウム教授(1944) ストールマン(1953) 誕生日
申し訳ありませんが、現在意見投稿をできない状態にしています。 |
たまには魔法使いらしく、異世界転移の魔法のことでも書こう。
ここは「魔法使いの森」だからね。
最初に転移魔法の術式から示してしまう。
今回の記事の目的は、この術式を解説することだから。
F(w) = ∫ f(t) e^(iwt) dt
まず、t は「この世界」を意味している。
具体的に言えば、時間によって変化していく世界。t は Time の意味だ。
転移後の世界は w で、これは「周波数」を意味している。
転移後の世界にはもはや時間はなく、周波数が支配する世界だ。
で、f(t) は転移させたいもの。F(w) が転移後の変化した姿。
この術式の主な目的は、「この世界」では強すぎて手も足も出ない敵を、転移させて よわよわ にして、その後で無双を楽しむことだ。
さて、転移の方法だが、術式に書かれた e^(iwt) というのが重要な部分だ。
この中で、t と w はすでに出てきた。時間と周波数だ。
並んで書かれているのは、この２つが密接な関係にあることを意味している。
というわけで、周波数の説明に移ろう。
すでに解っている人もいるかも知れないが、周波数とは「何かを繰り返すときの、一定時間での繰り返し回数」を意味している。
周波数の定義に時間が入っている。だから密接なのは当然で、不可分のものだ。
でも、並んで書く…掛け算を意味するのだけど、固定された w に対して、流れ続ける t をかけ合わせたら、結果の数は大きくなっていくだけだ。
周波数なのに「繰り返し」が出てこない。繰り返しはどこにあるのだろう。
ここで、e と i について説明する必要がある。この術式の最初の重要ポイントだ。
少し長くなるがお付き合いいただこう。
まず、i は √-1 のことだ。「自分自身を掛け合わせると、-1 になる数」だな。
i*i = -1 、と書き直すこともできる。でも、この数は普通は存在し得ない。
数には「同じものを掛け合わせると、必ずプラスになる」という性質があるためだ。
しかし、これは非常に都合が悪い。
我々の使う術式の体系は、完全性が求められる。
ある操作…ここでは √ という操作が決められたら、それは「すべての数」に適用できなくては完全とは言えない。
そこで、今まで知られていた数の体系を拡張し、「同じものを掛け合わせるとマイナスになる」という数を想定することにした。
それが i だ。虚数と呼ばれる。
…と、ここまで理解すると、当然次の疑問が出てくる。
√ は「完全性」を破綻させ、新たな数を想定する必要があった。
では、√i はどうなるのだろう。また破綻してしまうのではないか。
いや、幸いなことにそうではない。
i = ( (1+i) / √2 ) * ( (1+i) / √2 )
計算してみるとわかるが、この式は正しく、i を含む数の体系で √ は完全性を保つ。
1+i 、という形には、普通の数 1 と、虚数 i が入っている。
この形を、複素数と呼ぶ。
1 の部分を 2 , 3 と変化させられるように、i の部分も 2i , 3i というように変化させられる。
数は、直線上に表すことができる。これを数直線と呼ぶ。
しかし、虚数は数直線上には乗らず、独立した「虚数直線」を作る。
そして、複素数を表現するときは、数直線と虚数直線を直交させ、「複素数平面」を作る。
直交しているので、-1 と i は、0 を中心とした角度で言えば 90 度のところに位置する。
i = √-1
という式は、0 を中心に 90 度回転する操作なんだ。
先程 √i を複素数で示した。答えを複素数平面上に乗せると、回転が 45度になっていることがわかる。
√ によって、複素平面上で回転することができるんだ。
ここからは少し話を飛ばす。
√ を使えば、角度を半分づつ制御することができるが、もっと自由な角度に回転する方法が発見された。
e^(ix)
これで、角度が x のときの複素平面上の位置を計算できる。
ここで、e は「ネイピア数」と呼ばれるものだ。自然対数の底を意味する。
自然対数もまた面白い世界なのだが、ここでは詳細は扱わない。
話が長くなりすぎるからね。
今まで話に出てこなかった「自然対数」というものが急に顔を出してくるのは驚きなのだが、とにかくこれで自由な角度を示すことができるようになった。
さて、ここでやっと、最初の疑問に戻ることができる。
最初に書いた、異世界転移の術式をもう一度示そう。
F(w) = ∫ f(t) e^(iwt) dt
疑問は、wt は周波数…繰り返しを決めるもののはずなのに、掛け算だけでは大きくなる一方だ、ということだった。
その答えが、e^(iwt) 全体にある。
e^(ix) の形は、複素平面上で 0 を中心とした角度 x の位置にある、距離 1 の点を示すものだ。
簡単に言い換えれば x を変化させると「円を描く」。
円を描くのだから、当然繰り返しになる。wt は時間とともに大きくなるが、全体は繰り返すのだ。
このときの周波数は、w によって決まることになる。
この円こそが、異世界転移のための転移門となる、魔法陣だ。
魔法陣は円でなくてはならない。円は完全を意味するためだ。
もっとも、状況に応じて多少の装飾が行われる場合もある。
特定状況ではその方が効率が高まるためだが、今回は詳細に立ち入らない。
さて、魔法陣が描けたら、転移させたいものを魔法陣に載せる。
転移させたいものは、この世界 f(t) だった。
もう一度術式を示すと、
F(w) = ∫ f(t) e^(iwt) dt
魔法陣の隣に f(t) が並べられているのがわかる。
さて、ここでもう一度魔法陣に話を戻すと、これは複素平面上のものだ。
そのため、f(t) も複素平面に載る必要がある。
しかし、現実世界には虚数軸がない。
厳密にいえば、世界に虚数軸はあるのだ。
しかし、我々人間は、虚数軸方向の世界を感知することができない。
そのため、世界には虚数軸はないように思える。
こればかりは仕方がない。感じられないので、虚数軸は常に「0」でも入れておくことにしよう。
それでも複素平面に載りさえすれば大丈夫。
載せ方だが、術式の上では掛け算になっている。これは、ベクトルの内積を意味する。
内積は射影を意味するのだが…この理解が、異世界転移の術式の２番目のポイントとなる。
射影、「影がさす」というのはつまり、ある面の真上から光を当てたときに、別の面がどのような影を落とすか、という意味だ。
例えば、sin cos は、0 を中心とした、ある角度をもった長さ 1 の線に対して、座標軸に対する「射影」を求める操作になる。
意味が分かってもらえるだろうか？
これを、座標軸ではなく「２つの線」…ここでいう線というのはベクトルなのだが、原点を共有する２つのベクトルが作る射影が「内積」となる。
ここまではなんとなく理解できただろうか？
ここから、話はさらに飛んでいくので、いちいち立ち止まって理解しながら進んで欲しい。
さて、２つの線の長さが共に 1 である、という前提があった場合、内積は「同じ方向を向いているか」を示す指標となる。
直交する場合、内積は 0 になる。重なる場合、内積は 1 になる。
完全に逆方向を向いていると、-1 になる。
ここまでも大丈夫だろうか？ 繰り返すが、理解しながら進んで欲しい。
さて、再び術式を振り返ろう。
F(w) = ∫ f(t) e^(iwt) dt
「世界」と「魔法陣」の内積を、∫ ～ dt で囲んでいる。
これは、「すべての t について計算し、足し合わせよ」という意味だ。
ここで、魔法陣は時間とともに、一定の速度でぐるぐる回る。
「世界」の側は、時間とともに変わるが無秩序だ。
無秩序ということは、内積は時間によっては 0 になったり 1 になったり、-1 になったりする。
いや、そんなわかりやすい値はめったになく、0.8256 だったり、-0.2429 だったり、とにかく無秩序だろう。
それらを全部足すと、おそらくプラスとマイナスが打ち消しあい、 0 になる。
厳密に 0 でなかったとしても、それに近い値になるだろう。
本当に無秩序なら、ね。
実際には、本当の無秩序というのはなかなかあるものではない。
いろいろな事象が重なり合ってわかりにくくはなっているが、世の中は波でできているのだ。
昔の偉大な魔法使いも、こんな言葉を残している、
ともかく、魔法陣の周波数と、世界の周波数の重なりがあると、結果に秩序が現れる。
無秩序の場合は結果が 0 付近になるが、秩序があると十分に大きな値が返される。
このとき、値の大きさはその周波数成分の強さを意味する。
つまり、術式によって世界を形作る波の周波数は解析され、「特定の」周波数の成分の強さを知ることができる。
…ん？ 特定の？
繰り返しになるが術式を示す。
F(w) = ∫ f(t) e^(iwt) dt
ここで、術式で得られる F(w) は、「特定の」w についてのものだ。
異世界に転移するには「すべての」 w について操作を行い、完全な F を作り出さなくてはならない。
これには多大な計算力が必要になる。
「すべての t を足し合わせる」という操作を「すべての w について」行う必要があるのだ。
ここでは深く扱わないが、FFT とか DCT という改良型の術式があって、それらを使うと劇的に計算量が減る。
でも、基本はここに書かれた術式だ。
さて、なんでこんなややこしい術式が必要かというと、異世界転移で無双するためだ。
最後にそれについて記しておこう。
世の中みんな波だらけなのだが、この波には傾向があることが知られている。
いわゆる、1/f ゆらぎ、という現象だ。名前を聞いたことがある人もいるかもしれない。
ここでいう f は、w / 2π のことで、w とだいたい同じものだ。
（厳密にいえば、f が周波数で w を角周波数という）
1/f ゆらぎとは、周波数と振幅の関係性を示すものだ。
これによれば、周波数が高いほど振幅が小さくなり、「些細なもの」になる傾向にある。
これが異世界転移の利点の一つ。
実世界の「波」のままでは何が何だかわからなかった敵でも、周波数にすると重要な部分が見えてくる。
重要でない場合は、ばっさばっさと切り捨ててしまおう。
残ったのは、大切な部分だけを残して、いらない部分を切り捨てたデータだ。
これはデータの圧縮にすごく役立つ。
音楽とか、動画とか、すごく大きいデータを驚くほど小さく圧縮するのには、こうした技術が活躍している。
楽器とか、人の声とか、いろいろな「音」には特定の周波数領域がある。
人の声に注目したいとき、それ以外の周波数はノイズだろう。
波のままでは、何がノイズなのか全くわからない。
しかし、周波数に分解すると、どこにノイズがあるのか見えてくる。
さらに、人の声でも個人によって音の高低はある。
しかし、発声する際に特定の「同時に出される周波数の比率」とか、「時間による周波数の上げ下げ」などはあり、これは個人の声の高低とは別に、ある程度の共通性がある。
こうした部分に注目すると、機械に音声を認識させることができる。
こちらも、波のままではとても処理できないのだが、周波数に分解すると処理できる。
いずれにしても、波というのは捉えどころがなくて、どう処理してよいかわからない。
これが周波数空間に転移すると、自由自在に扱えるようになる。
これが無双でなくて何であろう。
ちなみに、「完全１２平均律から多少音程がずれたときに、補正してくれる」なんてソフトもある。
誰かの歌をそのソフトにかけると、周波数解析して、音程がずれているときには一番近い音に揃えて出力してくれるの。
音痴でも上手に聞こえる魔法のソフト、だな。
CD だと歌がうまいのに、LIVE だと…なんて人は ｺﾞﾆｮｺﾞﾆｮ。
もう 20 年以上前に、アメリカの歌手 Cher がこれを効果的な「エフェクト」として使って話題を呼び、世界的な大ヒット曲となった。
元々歌がうまい人で、音痴補正はいらない。
でも、これで「滑らかに音程を変える」歌い方を処理すると、声が階段状にカクカクと変化する、非常に不思議な歌声になるのだ。
通称 Cher Effect。一時期使われすぎて食傷気味になって消えたのだけど、20年たってまた最近使われるようになっている、気がする。
（先日ラジオでこのエフェクトを使っている歌を聞いた）
さて、ここらへんで終了するが、一応エイプリルフールのネタだ。
術式自体は、フーリエ変換という数式で、これを使うと実世界のデータを周波数空間に変換できるのは事実。
先日、微分積分について書いたときに、最後に「フーリエ変換についても書きたかったけどやめた」と書いた。
その話はそれで終わりだったのだけど、今朝「今日は４月１日」と気づいたときに、このくだらないネタを書く好機だと思ったのだ。
ギャグは解説しすぎると面白くないので、細かな解説は省いた。
単に数学的な説明が面倒だった、ともいう。
そういう点でも、説明しないことの言い訳ができる今日は好機だった。
別年同日の日記
申し訳ありませんが、現在意見投稿をできない状態にしています。 |
長男（高校２年）が、最近 n 次元物体に興味を持っている。
４次元超立方体とかそういうやつね。
ネットでいろいろ調べて、すでに僕より詳しい。
そして、「４次元物体の３次元切片」を、切断する軸の値を時間軸に置き換えてアニメーションする CG を Youtube で見つけ、「面白そう、描いてみたい」と言い出した。
…で、しばらく部屋に籠っていたかと思ったら、「いきなり４次元は難しそうなので、３次元の８面体を表示するプログラムを、Scratch で作ってみた」と言ってきた。
陰面処理はない。透視変換もしていなかった。
つまり、「面」はなく、辺で表現した物体を、３つの軸のうち１つを無くした射影として描くプログラム。
さらには、２軸でくるくる回転できるようにも作り、奥行きを線の太さで表すようにも改良した。
データを入れ替えれば、８面体だけでなく、立方体や４面体も描けることを示した。
（１２面体とか、きっと描けるけどデータを作るのが面倒だからとやらなかった）
そして、「２軸回転できるけど、回転順序によって影響を受けてしまう。任意の斜め軸で回転できるようにしたい」と言い始めた。
僕はそれほど 3D に詳しくない。
ゲームで 3D を使っていた時も、ライブラリに計算を任せていただけだ。
任意の斜め軸を設定するなら、ロール・ピッチ・ヨーのパラメーターで回転できるようにすると良いのではないかな、という程度のサジェストはできたが、それ以上の知識は持ち合わせていなかった。
そもそも、長男はまだ行列計算を習っていない。
回転行列を作って計算する、というのもピンとこない状態だ。
紙に図と計算式を描きながらどうすればよいのかとしばらく考えていたら…
先日セガが、内部のプログラマー勉強会で使った、という 140ページにもわたる 3D 計算数学のテキストを無償公開した。
あぁ、これは長男に読むことを勧めよう、と思っていたら、すでに学校の友達の間でも話題になっていたようで、帰りの電車の中でスマホで読んでみたと言う。
で、やはり行列も、三角関数の変形公式もわかっていないので、読み解くのが難しい、という状態だ。
しかし、我が家的には、なかなか良いタイミングで公開してくれた。
ネットで調べていても、３次元物体を自由に回転させたいなら、どうやら「クォータニオン」を学ぶ必要があるようだ、というところには行きついていた。
そして、わかりやすいという本のタイトルまでは検索していたのだ。後は買うかどうか、という段階。
そこにわかりやすいテキストが公開された形なので、長男としては一生懸命読んでいる。
ところで、僕がゲーム作っていた時は、クォータニオンというのは使っていなかったように思う。
内部計算も 3x4 の、座標移動付きの回転行列だったからね。
僕も、テキストにちょっと興味はあるのだが…
長いし、今の仕事では 3D を使う機会はなさそうなので、読まないように思う。
同じテーマの日記(最近の一覧)
別年同日の日記
16年 コンピューターが初めてプログラムを実行した日(1948)
申し訳ありませんが、現在意見投稿をできない状態にしています。 |